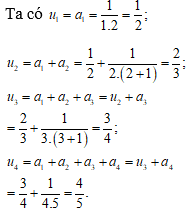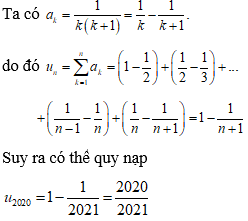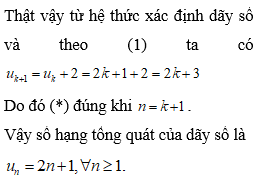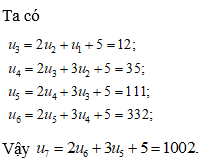30 câu hỏi trắc nghiệm thuộc Dạng 2: Tìm số hạng và xác định công thức số hạng tổng quát của dãy số có đáp án

Câu 1:

Cho dãy số $(a_{n})$ . Đặt $u_{n} = \sum_{k = 1}^{n} a_{k}$ với $a_{k} = \frac{1}{k (k + 1)}$ . Tính $u_{1}; u_{2}; u_{3}; u_{4} .$

Xem đáp án

Câu 2:

Cho dãy số $(a_{n})$ . Đặt $u_{n} = \sum_{k = 1}^{n} a_{k}$ với $a_{k} = \frac{1}{k (k + 1)} . Tính u_{2020}$

Xem đáp án

Câu 3:

Xác định công thức $u_{n} = \frac{n}{n + 1}; n \geq 1$ số hạng tổng quát u_n của dãy số $\{\begin{cases} u_{1} = 3 \\ u_{n + 1} = u_{n} + 2 \end{cases}$

Xem đáp án

Câu 4:

Cho dãy số

(u_{n})

được xác định như sau

\{\begin{cases} u_{1} = 1 \\ u_{n + 1} = u_{n} + 2 \end{cases}

. Tìm số hạng

u_{50}

.

Xem đáp án

Câu 5:

Cho dãy số

(u_{n})

được xác định như sau

\{\begin{cases} u_{1} = 1; u_{2} = 2 \\ u_{n + 2} = 2 u_{n + 1} + 3 u_{n} + 5 \end{cases}

. Tìm số hạng u₇.

Xem đáp án

Câu 6:

Cho dãy số

(u_{n})

xác định bởi

\{\begin{cases} u_{1} = 1 \\ u_{n + 1} = \frac{u_{n} + 2}{u_{n} + 1} \end{cases}

. Tìm số hạng u₈.

Xem đáp án

Ta có

u_{2} = \frac{u_{1} + 2}{u_{1} + 1} = \frac{1 + 2}{1 + 1} = \frac{3}{2}; u_{3} = \frac{u_{2} + 2}{u_{2} + 1} = \frac{\frac{3}{2} + 2}{\frac{3}{2} + 1} = \frac{7}{5}; u_{4} = \frac{u_{3} + 2}{u_{3} + 1} = \frac{\frac{7}{5} + 2}{\frac{7}{5} + 1} = \frac{17}{12}; u_{5} = \frac{u_{4} + 2}{u_{4} + 1} = \frac{\frac{17}{12} + 2}{\frac{17}{12} + 1} = \frac{41}{29}; u_{6} = \frac{u_{5} + 2}{u_{5} + 1} = \frac{\frac{41}{29} + 2}{\frac{41}{29} + 1} = \frac{99}{70}; u_{7} = \frac{u_{6} + 2}{u_{6} + 1} = \frac{\frac{99}{70} + 2}{\frac{99}{70} + 1} = \frac{239}{169};

Vậy

u_{8} = \frac{u_{7} + 2}{u_{7} + 1} = \frac{\frac{239}{169} + 2}{\frac{239}{169} + 1} = \frac{577}{408};

Câu 7:

Cho dãy số $(u_{n})$ với $\{\begin{cases} u_{1} = - 1 \\ u_{n + 1} = \frac{u_{n}}{2} \end{cases}$ .Tìm công thức của số hạng tổng quát.

Xem đáp án

Ta có $\{\begin{cases} u_{1} = - 1 \\ u_{2} = \frac{u_{1}}{2} \\ ... \\ u_{n} = \frac{u_{n - 1}}{2} \end{cases}$

Nhân vế với vế của các đẳng thức trên, ta được $u_{1} . u_{2} . u_{3} ... u_{n} = (- 1) . \frac{u_{1} . u_{2} . u_{3} ... u_{n - 1}}{\underset{n - 1 sè 2}{\underset{⏟}{2.2.2...2}}} \Leftrightarrow u_{n} = (- 1) . \frac{1}{2^{n - 1}} = (- 1) . {(\frac{1}{2})}^{n - 1}$

Vậy $u_{n} = (- 1) . {(\frac{1}{2})}^{n -} .$

Câu 8:

Cho dãy số $(u_{n})$ với $\{\begin{cases} u_{1} = - 1 \\ u_{n + 1} = \frac{u_{n}}{2} \end{cases}$ . Tính số hạng thứ 10 của dãy số.

Xem đáp án

Số hạng thức 10 của dãy là

u_{10} = (- 1) . {(\frac{1}{2})}^{9} = - \frac{1}{512} .

Câu 9:

Dãy số $(u_{n})$ được xác định bằng công thức $\{\begin{cases} u_{1} = 1 \\ u_{n + 1} = u_{n} + n^{3'} \end{cases} n \geq 1$ . Tìm công thức của số hạng tổng quát.

Xem đáp án

Ta có $u_{n + 1} = u_{n} + n^{3} \Rightarrow u_{n + 1} - u_{n} = n^{3} .$ Từ đó suy ra

$\begin{array}{l} u_{1} = 1; \\ u_{2} - u_{1} = 1^{3}; \\ u_{3} - u_{2} = 2^{3}; \\ ... \\ u_{n - 1} - u_{n - 2} = {(n - 2)}^{3}; \\ u_{n} - u_{n - 1} = {(n - 1)}^{3} . \end{array}$

Cộng từng vế các đẳng thức trên ta được

$\begin{array}{l} u_{1} + u_{2} - u_{1} + u_{1} - u_{2} + ... + u_{n - 1} - u_{n - 2} + u_{n} - u_{n - 1} \\ = 1 + 1^{3} + 2^{3} + 3^{3} + ... + {(n - 2)}^{3} + {(n - 1)}^{3} \\ \Leftrightarrow u_{n} = 1 + 1^{3} + 2^{3} + 3^{3} + ... + {(n - 2)}^{3} + {(n - 1)}^{3} \end{array}$

Bằng phương pháp quy nạp ta chứng minh được

$1^{3} + 2^{3} + 3^{3} + ... + {(n - 1)}^{3} = \frac{{(n - 1)}^{2} . n^{2}}{4}$

Vậy

u_{n} = 1 + \frac{n^{2} {(n - 1)}^{2}}{4}

Câu 10:

Dãy số $(u_{n})$ được xác định bằng công thức $\{\begin{cases} u_{1} = 1 \\ u_{n + 1} = u_{n} + n^{3'} \end{cases} n \geq 1$ . Tính số hạng thứ 30 của dãy số.

Xem đáp án

Số hạng thứ 30 của dãy số là

u_{30} = 1 + \frac{30^{2} {.29}^{2}}{4} = 189226

Câu 11:

Cho dãy số $(u_{n})$ , biết $u_{1} = 3; u_{n + 1} = \sqrt{1 + u_{n}^{2}} với n \geq 1$ .Viết năm số hạng đầu tiên của dãy số.

Xem đáp án

Ta có

$\begin{array}{l} u_{2} = \sqrt{1 + u_{1}^{2}} = \sqrt{10}; u_{3} = \sqrt{1 + u_{2}^{2}} = \sqrt{11}; \\ u_{4} = \sqrt{1 + u_{3}^{2}} = \sqrt{12}; u_{5} = \sqrt{1 + u_{4}^{2}} = \sqrt{13}; \end{array}$

Câu 12:

Cho dãy số $(u_{n})$ , biết $u_{1} = 3; u_{n + 1} = \sqrt{1 + u_{n}^{2}} với n \geq 1$ .Dự đoán công thức số hạng tổng quát và chứng minh bằng phương pháp quy nạp.

Xem đáp án

Câu 13:

Cho dãy số

(u_{n})

có

u_{1} = 7; u_{n + 1} = 2 u_{n} + 3.

Khi đó u₃ bằng

A. 17

B. 77

C. 37

D. 9

Xem đáp án

Chọn C

Ta có

u_{3} = 2 u_{2} + 3 = 2. (2 u_{1} + 3) + 3 = 4 u_{1} + 9 - 4.7 + 9 = 37.

Câu 14:

Số 7922 là số hạng thứ bao nhiêu của dãy số

u_{n} = n^{2} + 1 ?

A. 79

B. 89

C. 69

D. 99

Xem đáp án

Chọn B

Ta có $7922 = 7921 + 1 = 89^{2} + 1 \Rightarrow n = 89$

Câu 15:

Cho dãy số

(u_{n})

có

u_{n} = - n^{2} + n + 1

. Số -19 là số hạng thứ mấy của dãy?

A. 5

B. 7

C. 6

D. 4

Xem đáp án

Chọn A

Giả sử $u_{n} = - 19 (n \in ℕ^{*})$

Suy ra $- n^{2} + n + 1 = - 19 \Leftrightarrow - n^{2} + n + 20 = 0 \Leftrightarrow [\begin{array}{l} n = 5 \\ n = - 4 \end{array} \Leftrightarrow n = 5$ (do $n \in ℕ *$ ).

Vậy số -19 là số hạng thứ 5 của dãy

Câu 16:

Cho dãy số $u_{n} = \frac{n^{2} + 2 n - 1}{n + 1}$ . Giá trị u₁₁ là

A. $u_{11} = \frac{182}{12} .$

B. $u_{11} = \frac{1142}{12} .$

C. $u_{11} = \frac{1422}{12} .$

D. $u_{11} = \frac{71}{6} .$

Xem đáp án

Chọn D

Ta có

u_{11} = \frac{11^{2} + 2.11 - 1}{11 + 1} = \frac{71}{6}

Câu 17:

Cho dãy số

(u_{n})

xác định bởi

\{\begin{cases} u_{1} = 2 \\ u_{n + 1} = u_{n} + 5, n \in ℕ^{*} \end{cases}

. Giá trị u₁₀ là

A. 57

B. 62

C. 47

D. 52

Xem đáp án

Chọn C

Từ $\{\begin{cases} u_{1} = 2 \\ u_{n + 1} = u_{n} + 5, n \in ℕ^{*} \end{cases}$ , ta có $u_{n + 1} - u_{n} = 5$

=> dãy $(u_{n})$ là một cấp số cộng với công sai d=5 nên $u_{10} = u_{1} + 9 d = 2 + 45 = 47$

Câu 18:

Cho dãy số có các số hạng đầu là 8, 15, 22, 29, 36,… Số hạng tổng quát của dãy số này là

A. $u_{n} = 7 n + 7.$

B. $u_{n} = 7. n .$

C. $u_{n} = 7. n + 1.$

D. $u_{n} = n + 7 .$

Xem đáp án

Chọn C

Ta có $8 = 7.1 + 1; 15 = 7.2 + 1; 22 = 7.3 + 1; 29 = 7.4 + 1; 36 = 7.5 + 1$

Suy ra số hạng tổng quát $u_{n} = 7 n + 1$

Câu 19:

Cho dãy số có các số hạng đầu là

0; \frac{1}{2}; \frac{2}{3}; \frac{3}{4}; \frac{4}{5}; ...

Số hạng tổng quát của dãy số này là

A. $u_{n} = \frac{n + 1}{n} .$

B. $u_{n} = \frac{n}{n + 1} .$

C. $u_{n} = \frac{n - 1}{n} .$

D. $u_{n} = \frac{n^{2} - n}{n + 1} .$

Xem đáp án

Chọn B

Ta có $0 = \frac{0}{0 + 1}; \frac{1}{2} = \frac{1}{1 + 1}; \frac{2}{3} = \frac{2}{2 + 1}; \frac{3}{4} = \frac{3}{3 + 1}; \frac{4}{5} = \frac{4}{4 + 1}$

Suy ra $u_{n} = \frac{n}{n + 1} .$

Câu 20:

Cho dãy số

(u_{n})

với

u_{n} = 2 n + 1

. Số hạng thứ 2019 của dãy là

A. 4039

B. 4390

C. 4930

D. 4093

Xem đáp án

Chọn A

Ta có

u_{2019} = 2.2019 + 1 = 4039

Câu 21:

Cho dãy số

(u_{n})

có số hạng tổng quát

u_{n} = \frac{2 n + 1}{n + 2}

. Số

\frac{167}{84}

là số hạng thứ mấy của dãy?

A. 300

B. 212

C. 250

D. 249

Xem đáp án

Chọn C

Ta có $u_{n} = \frac{167}{84} \Leftrightarrow \frac{2 n + 1}{n + 2} = \frac{167}{84} \Leftrightarrow 84 (2 + 1) = 167 (n + 2) \Leftrightarrow n = 250$

Vậy $\frac{167}{84}$ là số hạng thứ 250 của dãy số $(u_{n})$

Câu 22:

Cho dãy số

(u_{n})

với

u_{n} = \frac{a n^{2}}{n + 1}

(a là hằng số). Hỏi u_n+1 là số hạng nào sau đây?

A. $u_{n + 1} = \frac{a . {(n + 1)}^{2}}{n + 2} .$

B. $u_{n + 1} = \frac{a . {(n + 1)}^{2}}{n + 1} .$

C. $u_{n + 1} = \frac{a . n^{2} + 1}{n + 1} .$

D. $u_{n + 1} = \frac{a . n^{2}}{n + 2} .$

Xem đáp án

Chọn A

Ta có $u_{n + 1} = \frac{a . {(n + 1)}^{2}}{(n + 1) + 1} = \frac{a {(n + 1)}^{2}}{n + 2}$

Câu 23:

Cho dãy số

(u_{n})

với

\{\begin{cases} u_{1} = 5 \\ u_{n + 1} = u_{n} + n \end{cases} .

Số hạng tổng quát u_n của dãy số là số hạng nào dưới đây?

A. $u_{n} = \frac{(n - 1) n}{2} .$

B. $u_{n} = 5 + \frac{(n - 1) n}{2} .$

C. $u_{n} = 5 + \frac{(n + 1) n}{2} .$

D. $u_{n} = 5 + \frac{(n + 1) (n + 2)}{2} .$

Xem đáp án

Chọn B

Ta có

u_{n} = 5 + 1 + 2 + 3 + ... + n - 1 = 5 + \frac{n (n - 1)}{2}

Câu 24:

Cho dãy số

(u_{n})

được xác định như sau

\{\begin{cases} u_{1} = 0 \\ u_{n + 1} = \frac{n}{n + 1} (u_{n} + 1) \end{cases} .

Số hạng u₁₁ là

A. $u_{11} = \frac{11}{2} .$

B. $u_{11} = 4.$

C. $u_{11} = \frac{9}{2} .$

D. $u_{11} = 5 .$

Xem đáp án

Chọn D

\begin{array}{l} u_{2} = \frac{1}{2} (u_{1} + 1) = \frac{1}{2}; u_{3} = \frac{2}{3} (u_{2} + 1) = 1; u_{4} = \frac{3}{4} (u_{3} + 1) = \frac{3}{2}; \\ u_{5} = \frac{4}{5} (u_{4} + 1) = 2; u_{6} = \frac{5}{6} (u_{5} + 1) = \frac{5}{2}; u_{7} = \frac{6}{7} (u_{6} + 1) = 3; \\ u_{8} = \frac{7}{8} (u_{7} + 1) = \frac{7}{2}; u_{9} = \frac{8}{9} (u_{8} + 1) = 4; u_{10} = \frac{1}{2} (u_{9} + 1) = \frac{9}{2}; \\ u_{11} = \frac{10}{11} (u_{10} + 1) = 5; \end{array}

Câu 25:

Cho dãy số

(u_{n})

với

\{\begin{cases} u_{1} = 1 \\ u_{n + 1} = u_{n} + 2 n + 1, n \in ℕ^{*} \end{cases} .

Số hạng tổng quát u_n là

A. $u_{n} = n^{2} .$

B. $u_{n} = 2 n^{2} .$

C. $u_{n} = n^{2} + 1 .$

D. $u_{n} = 3 n^{2} - 1 .$

Xem đáp án

Chọn A

Ta có $u_{1} = 1; u_{2} = u_{1} + 3; u_{3} = u_{2} + 5; u_{4} = u_{3} + 7; . . .; u_{n} = u_{n - 1} + (2 n - 1)$

Cộng từng vế với vế của các đẳng thức trên và rút gọn ta được $u_{n} = 1 + 3 + 5 + 7 + ... + (2 n - 1) = n^{2} .$

Câu 26:

Cho dãy số

(u_{n})

với

u_{n} = \frac{n - 1}{n^{2} + 1}

, biết

u_{k} = \frac{2}{13} .

Hỏi u_k là số hạng thứ mấy của dãy số đã cho?

A. Thứ năm.

B. Thứ sáu.

C. Thứ ba.

D. Thứ tư.

Xem đáp án

Chọn A

$u_{k} = \frac{k - 1}{k^{2} + 1} \Rightarrow \frac{k - 1}{k^{2} + 1} = \frac{2}{13} \Rightarrow k = 5$ (do $k \in ℕ^{*}$ ).

Câu 27:

Cho dãy

(u_{n})

xác định bởi

u_{1} = \frac{1}{2} và u_{n} = u_{n - 1} + 2 n

với mọi

n \geq 2

. Số hạng u₅₀ bằng

A. 1274,5

B. 2548,5

C. 5096,5

D. 2550,5

Xem đáp án

Chọn B

Ta có

$\{\begin{cases} u_{1} = \frac{1}{2} \\ u_{2} = u_{1} + 2 \\ u_{3} = u_{2} + 4 \\ ... \\ u_{49} = u_{48} + 2.49 \\ u_{50} = u_{49} + 2.50 \end{cases}$

Cộng vế với vế các đẳng thức trên, ta được $u_{50} = \frac{1}{2} + 2 (2 + 3 + ... + 50) = \frac{1}{2} + 2 (25.51 - 1) = 2548,5$ .

Câu 28:

Cho dãy số có các số hạng đầu là 0,1; 0,001; 0,001; 0,0001;… Số hạng tổng quát của dãy số có dạng

A. $u_{n} = \underset{n ch÷ sè 0}{\underset{⏟}{0,00...01}} .$

B. $u_{n} = \underset{n - 1 ch÷ sè 0}{\underset{⏟}{0,00...01}} .$

C. $u_{n} = \frac{1}{10^{n - 1}} .$

D. $u_{n} = \frac{1}{10^{n + 1}} .$

Xem đáp án

Chọn A

Ta có

Số hạng thứ 1 có 1 chữ số 0;

Số hạng thứ 2 có 2 chữ số 0;

Số hạng thứ 3 có 3 chữ số 0;

…

Suy ra $u_{n}$ có n chữ số 0.

Công thức số hạng tổng quát của dãy số là $u_{n} = \frac{1}{10^{n}} = \underset{n ch÷ sè 0}{\underset{⏟}{0,00...01}}$

Câu 29:

Số hạng âm trong dãy số

x_{1}; x_{2}; x_{3}; ...; x_{n}

với

x_{n} = C_{n + 5}^{4} - \frac{143 P_{n + 5}}{96 P_{n + 3}}

là

A. $x_{1}; x_{2} .$

B. $x_{1}; x_{2}; x_{3} .$

C. $x_{1}; x_{2}; x_{3} ... x_{n} .$

D. $x_{1}; x_{2}; x_{3}; x_{4} .$

Xem đáp án

Chọn B

Ta có $c_{n + 5}^{4} = \frac{(n + 5) (n + 4) (n + 3) (n + 2)}{24}, \frac{143 P_{n + 5}}{96 P_{n + 3}} = \frac{143 (n + 5) (n + 4)}{96} x_{n} = C_{n + 5}^{4} - \frac{143 P_{n + 5}}{96 P_{n + 3}} = \frac{(n + 5) (n + 4) (2 n + 17) (2 n - 7)}{96} > 0, \forall n \geq 4, n \in ℕ^{*}$

Vậy các số hạng âm là $x_{1}; x_{2}; x_{3}$ .

Câu 30:

Cho dãy số

(u_{n})

được xác định bởi

\{\begin{cases} u_{1} = 2 \\ u_{n + 1} - u_{n} = 2 n - 1 \end{cases}

. Số hạng tổng quát u_n của dãy số là

A. $u_{n} = n^{2} + 1.$

B. $u_{n} = n^{2} + 2 .$

C. $u_{n} = 2 + {(n + 1)}^{2} .$

D. $u_{n} = 2 - {(n - 1)}^{2} .$

Xem đáp án

Chọn A

Ta có

$\{\begin{cases} u_{1} = 2 \\ u_{2} = u_{1} + 2.2 - 1; \\ u_{3} = u_{2} + 2.3 - 1; \\ ... \\ u_{n} = u_{n - 1} + 2. n - 1 \end{cases}$

Cộng vế với vế của các đẳng thức trên rồi rút gọn, ta được $u_{n} = 2 + 2. (2 + 3 + ... + n) - (n - 1) = 2 + (n - 1) (n + 2) - n + 1 = n^{2} + 1$