- Đề số 1
- Đề số 2
- Đề số 3
- Đề số 4
- Đề số 5
- Đề số 6
- Đề số 7
- Đề số 8
- Đề số 9
- Đề số 10
- Đề số 11
- Đề số 12
- Đề số 13
- Đề số 14
- Đề số 15
- Đề số 16
- Đề số 17
- Đề số 18
- Đề số 19
- Đề số 20
- Đề số 21
- Đề số 22
- Đề số 23
- Đề số 24
- Đề số 25
- Đề số 26
- Đề số 27
- Đề số 28
- Đề số 29
- Đề số 30
- Đề số 31
- Đề số 32
- Đề số 33
- Đề số 34
- Đề số 35
- Đề số 36
- Đề số 37
- Đề số 38
- Đề số 39
- Đề số 40
- Đề số 41
- Đề số 42
- Đề số 43
- Đề số 44
- Đề số 45
- Đề số 46
- Đề số 47
- Đề số 48
- Đề số 49
- Đề số 50
- Đề số 51
- Đề số 52
- Đề số 53
- Đề số 54
- Đề số 55
- Đề số 56
- Đề số 57
- Đề số 58
- Đề số 59
- Đề số 60
- Đề số 61
- Đề số 62
- Đề số 63
- Đề số 64
- Đề số 65
- Đề số 66
- Đề số 67
- Đề số 68
- Đề số 69
- Đề số 70
- Đề số 71
- Đề số 72
- Đề số 73
- Đề số 74
- Đề số 75
- Đề số 76
- Đề số 77
- Đề số 78
- Đề số 79
- Đề số 80
- Đề số 81
- Đề số 82
- Đề số 83
- Đề số 84
- Đề số 85
Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 10)
-
12942 lượt thi
-
56 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Lời giải
Để A ∩ B = Ø
\( \Leftrightarrow \left[ \begin{array}{l}m + 5 < - 1\\m > 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m < - 6\\m > 3\end{array} \right. \Leftrightarrow - 6 \le m \le 3\)
Vậy để A giao B bằng rỗng thì –6 ≤ m ≤ 3.
Câu 2:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: C
Để có hình chiếu vuông góc các tia chiếu phải xiên góc hoặc vuông góc với mặt phẳng hình chiếu.
Câu 3:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: B
Hình chiếu vuông góc là hình biểu diễn thu được từ phép chiếu song song.Câu 4:
Cho đường thẳng mx + (2 – 3m)y + m – 1= 0 (d)
a) Tìm điểm cố định mà đường thẳng (d) luôn đi qua.
b) Tìm m để khoảng cách từ gốc O đến đường thẳng (d) lớn nhất.
 Xem đáp án
Xem đáp án
Lời giải
a) Gọi I (x0; y0) là điểm cố định mà đường thẳng (d) luôn đi qua với điểm m nên ta có: mx0 + (2 – 3m)y0 + m – 1 = 0 \(\forall m\)
⇔ m(x0 – 3y0 + 1) + 2y0 – 1 = 0 \(\forall m\)
\( \Leftrightarrow \left\{ \begin{array}{l}{x_0} - 3{y_0} + 1 = 0\\2{y_0} - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = \frac{1}{2}\\{y_0} = \frac{1}{2}\end{array} \right.\)
⇔ \(I\left( {\frac{1}{2};\frac{1}{2}} \right)\).
b) Gọi H là hình chiếu vuông góc của O lên đường thẳng (d).
Ta có: OH ≤ OI nên OH lớn nhất bằng OI khi và chỉ khi H ≡ I hay OI ⊥ (d). Đường thẳng qua O có phương trình u = ax do \(I\left( {\frac{1}{2};\frac{1}{2}} \right) \in OI \Rightarrow \frac{1}{2} = \frac{1}{2}a\).
Suy ra a = 1.
Do đó OI: y = x.
Đường thẳng (d) được viết lại như sau:
mx + (2 – 3m)y + m – 1 = 0
⇔ (2 – 3m)y = –mx + 1 – m
• Nếu \(m = \frac{2}{3}\) thì đường thẳng (d): \(x - \frac{1}{2} = 0\) song song với trục Oy nên khoảng cách từ O đến (d) là \(\frac{1}{2}\).
• Nếu \(m \ne \frac{2}{3}\) đường thẳng (d) có thể viết lại \(y = \frac{m}{{3m - 2}}x + \frac{{m - 1}}{{3m - 2}}\).
Điều kiện để (d) vuông góc với OI là: \(\frac{m}{{3m - 2}}.1 = - 1\)
\( \Leftrightarrow m = 2 - 3m \Leftrightarrow m = \frac{1}{2}\).
Khi đó \(OI = \sqrt {{{\left( {\frac{1}{2}} \right)}^2} + {{\left( {\frac{1}{2}} \right)}^2}} = \frac{{\sqrt 2 }}{2}\).
Vậy \(m = \frac{1}{2}\) thỏa mãn yêu cẩu bài toán.Câu 5:
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: A
Gọi x ≥ 0, y ≥ 0 lần lượt là số tấm bìa cắt theo cách thứ nhất, thứ hai.
Bài toán đưa đến tìm x ≥ 0, y ≥ 0 thỏa mãn hệ:
\(\left\{ \begin{array}{l}3x + 2y \ge 900\\x + 3y \ge 1000\\6x + y = 900\end{array} \right.\) sao cho L = x + y nhỏ nhất.
Trong mặt phẳng tọa độ Oxy, vẽ các đường thẳng:
(d): 3x + 2y – 900 = 0;
(d’): x + 3y – 1 000 = 0;
(∆): 6x + y – 900 = 0.
Khi đó miền nghiệm của hệ bất phương trình (*) nửa đường thẳng BC nằm trong phần tô màu trên hình vẽ.

Suy ra L = x + y nhỏ nhất đạt được tại điểm B.
Khi đó, L(x; y) = L(100; 300).
Câu 6:
a) Chứng minh: AMNB là hình thang cân;
b) Chứng minh: MNPD là hình bình hành;
c) Chứng minh: DM vuông góc AN.
 Xem đáp án
Xem đáp án
Lời giải
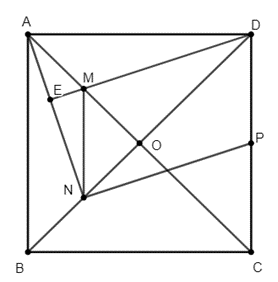
a) Vì MN là đường trung bình của ∆OAB nên MN // AB.
Suy ra AM = NB = \(\frac{1}{2}OA = \frac{1}{2}OB\).
Do đó tứ giác MNBA là hình thang cân.
b) Ta có MN // AB nên MN // DP
Do đó MN = \(\frac{1}{2}AB = \frac{1}{2}DC = DP\).
Vậy tứ giác MNPD là hình bình hành.
c) Xét ∆DMB có MO vừa là đường trung tuyến vừa là đường cao.
Suy ra DMB là tam giác cân.
Do đó \(\widehat {MBD} = \widehat {MDB}\) (1)
Dễ thấy: ∆OAN = ∆OBM suy ra \(\widehat {MBO} = \widehat {OAN}\) (2)
Từ (1) và (2) suy ra \(\widehat {OAN} = \widehat {MDB}\).
Mà \(\widehat {DNP} = \widehat {MDB}\) (hai góc so le trong)
Suy ra \(\widehat {DNP} = \widehat {OAN}\).
Xét ∆OAN có \(\widehat {OAN} + \widehat {ONA} = 90^\circ \)
\( \Rightarrow \widehat {DNP} + \widehat {ONA} = 90^\circ \)\( \Rightarrow \)NP\( \bot \)AN.
Mà DM // ND suy ra DM\( \bot \)AN.Câu 7:
Cho ∆ABC nhọn (AB < AC). Đường tròn tâm O, đường kính BC lần lượt cắt AB, AC tại M và N; BM và CN giao nhau tại H, AH cắt BC tại K.
a) Chứng minh: AK ⊥ BC.
b) Chứng minh: AM . AB = AN . AC.
 Xem đáp án
Xem đáp án
Lời giải
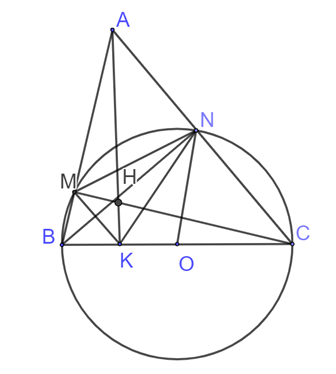
a) Do N ∈ (O) ⇒ \(ON = \frac{1}{2}BC\)⇒ BN ⊥ AC;
M ∈ (O) ⇒ \[MO = \frac{1}{2}BC\] ⇒ MC ⊥ AB.
⇒ H là giao điểm của đường cao
⇒ AH ⊥ BC
⇒ AK ⊥ BC.
b) Xét ∆ANB và ∆AMC có
\[\widehat {BAC}\]là góc chung
\[\widehat {ANB} = \widehat {AMC}\](= 90°)
Do đó ∆ANB ᔕ ∆AMC (g.g).
Suy ra \[\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}\] (các cạnh tương ứng tỉ lệ).
Vậy AM . AB = AN. AC (đpcm).
Câu 8:
 Xem đáp án
Xem đáp án
Lời giải
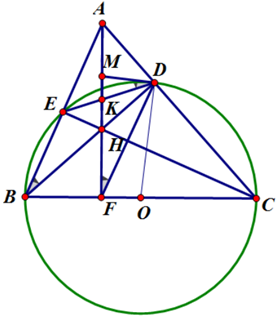
Ta có \[\widehat {BDC} = \widehat {BEC}\] = 90° (góc nội tiếp chắn nửa đường tròn).
Vì BD và CE là đường cao của ∆ABC mà BD và CE cắt nhau tại H nên H là trực tâm của ∆ABC.
Suy ra AH ⊥ BC hay\[\widehat {AFB} = \widehat {ADB}\]= 90°.
Do đó, đỉnh D, F cùng nhìn A, B dưới góc 90°.
Suy ra tứ giác ABFD nội tiếp ⇒ \[\widehat {ABD} = \widehat {AFD}\] (góc nội tiếp cùng chắn cung AD).
Lại có ∆ADH vuông tại D; M là trung điểm của AH.
⇒ DM là đường trung tuyến ứng cạnh huyền
⇒ DM = AM
⇒ \[\widehat {MAD} = \widehat {MDA}\]
Mà OD = OC nên ∆ODC cân suy ra \[\widehat {OCD} = \widehat {ODC}\]
Do đó \[\widehat {OCD} = \widehat {MAD} = \widehat {MDA} + \widehat {ODC}\].
Do AF⊥BC ⇒ \[\widehat {MAD} + \widehat {ODC} = 90^\circ \]
⇒ \[\widehat {MDA} + \widehat {ODC} = 90^\circ \]⇒ \[\widehat {MDO} = 90^\circ \] ⇒ MD là tiếp tuyến của (O)
⇒ \[\widehat {ABF} + \widehat {MDE}\] (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây chắn cung
ED).
⇒ \[\widehat {AFD} + \widehat {MDE}\] ⇒ MDK ᔕ ∆MFD (g.g).
⇒ \[\frac{{MD}}{{MF}} = \frac{{MK}}{{MD}}\] ⇒ MD2 = MK . MF.
Câu 9:
Cho ∆ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với H qua AB, gọi E là điểm đối xứng với H qua AC.
a) Chứng minh rằng D đối xứng với E qua A.
b) Tam giác DHE là tam giác gì? Vì sao?
c) Tứ giác BDEC là hình gì? Vì sao?
d) Chứng minh rằng BC = BD + CE.
 Xem đáp án
Xem đáp án
Lời giải
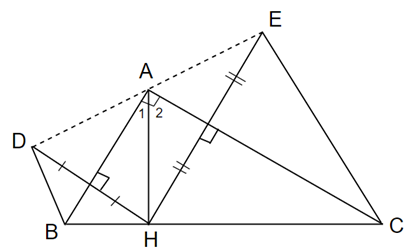
a) Vì D đối xứng với H qua AB nên AB là đường trung trực của DH
nên AH = AD (1)
Vì E đối xứng với H qua AC nên AC là đường trung trực của HE
nên AH = AE (2)
Từ (1) và (2) ⇒ AD = AE (3)
Mặt khác: \[\widehat {DBA} = \widehat {BAH}\]; \[\widehat {HAC} = \widehat {CAE}\]
\[\widehat {BAH} = \widehat {HAC}\] = 90°
Do đó \[\widehat {DAB} + \widehat {BAH} + \widehat {HAC} + \widehat {CAE}\] = 180°
Tức là ba điểm D, A, E thẳng hàng (4)
Từ (3) và (4) suy ra D và E đối xứng với nhau qua A.
b) ∆ DHE có HA là trung tuyến và \[HA = \frac{1}{2}DE\] nên ∆DHE vuông tại H.
c) Ta có: ∆ADB = ∆AHB (c.c.c)
Suy ra \[\widehat {ADB} = \widehat {AHB}\] = 90°
Tương tự có \[\widehat {AEC}\] = 90°
⇒ BD // CE (cùng vuông góc với DE)
Nên tứ giác BAEC là hình thang có 2 góc vuông kề cạnh bên DE.
Do đó tứ giác BAEC là hình thang vuông.
d) Do AB là đường trung trực của DH nên BD = BH (5)
Do AC là đường trung trực của EH nên CE = CH (6)
Cộng vế với vế của (5) và (6) ta suy ra BD + CE = BH + CH.
Hay BD + CE = BC.
Câu 10:
 Xem đáp án
Xem đáp án
Lời giải
12 giờ trưa là: 12 . 60 = 720 phút (tính từ 0 giờ).
10 giờ sáng là: 10 . 60 = 600 phút (tính từ 0 giờ).
Gọi a là số cần tìm.
Khi đó: 720 – x – 9 = 600 + 2x
711 – x = 600 + 2x
2x + x = 711 – 600
3x = 111
x = 37.
Câu 11:
 Xem đáp án
Xem đáp án
Lời giải
Ta có gốc tọa độ O(0; 0)
Nên \[\overrightarrow {AO} = \left( {5;--\,3} \right)\], \[\overrightarrow {OB} = \left( {--\,4;--\,6} \right)\]
\[\overrightarrow {AO} .\overrightarrow {OB} \] = 5 . (– 4) + (–3) . (–6) = –2.
Câu 12:
 Xem đáp án
Xem đáp án
Lời giải
\[\overrightarrow {AB} = (4; - 3) = ({x_1};{x_2})\]
\[\overrightarrow {BC} = ( - 6; - 5) = ({y_1};{y_2})\]
\[ \Rightarrow \overrightarrow {AB} \,.\,\overrightarrow {BC} = {x_1}\,.\,{y_1} + {x_2}.{y_2} = 4\,.\,( - \,6) + ( - \,3)\,.\,( - \,5) = - \,9\].
Câu 13:
a) Tìm các bội của 3.
b) Tìm các ước của –15.
c) Tìm các bội của –3.
d) Tìm các ước của 15.
 Xem đáp án
Xem đáp án
Lời giải
a) Các bội của 3 là:
B(3) = {0; 3; –3; 6; –6; 9; –9 ; ...}.
b) Các ước của 15 là:
Ư(–15) = {1; –1; 3; –3; 5; –5; 15; –15}.
c) Các bội của –3 là:
B(–3)= {0; 3; –3; 6; –6; 9; –9 ;...}.
d) Các ước của 15 là:
Ư(15) = {1; –1; 3; –3; 5; –5; 15; –15}.
Câu 14:
 Xem đáp án
Xem đáp án
Lời giải
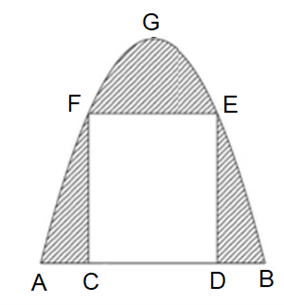
Đỉnh G có tọa độ (0; 4) nên a . 02 + b . 0 + c = 4
Do đó c = 4.
Điểm D có tọa độ (2; 3) nên a . 22 + b . 2 + 4 = 3
⇔ 4a + 2b = −14 (1)
Điểm C có tọa độ (–2; 3) nên a . (−2)2 + b . (−2) + 4 = 3
⇔ 4a – 2b = −14 (2)
Từ (1) và (2) suy ra a = – 0,25; b = 0.
Khi đó parabol có dạng y = −0,25 . x2 + 4
Điểm A và B có tung độ y = 0
⇔ −0,25 . x2 + 4 = 0
⇔ x = 4 hoặc x = – 4
Suy ra điểm B có tọa độ (4; 0) và điểm A có tọa độ (– 4; 0).
Vậy khoảng cách giữa hai điểm A và B là 8.
Câu 15:
 Xem đáp án
Xem đáp án
Lời giải
Ta có x3 − 2x2 + 5x = x( x2 − 2x + 5).
Câu 16:
 Xem đáp án
Xem đáp án
Lời giải
Nhóm hai số hạng đầu tiên và hai số hạng cuối.
(x3 + 2x2) − 5x − 10
Đưa ước số chung lớn nhất (ƯCLN) từ từng nhóm ra ngoài.
x2(x + 2) − 5(x + 2)
Phân tích đa thức thành thừa số bằng cách đưa ước số chung lớn nhất ra ngoài, ta được:
x2(x + 2) − 5(x + 2) = (x + 2)(x2 − 5)
Vậy x3 + 2x2 – 5x – 10 = (x + 2)(x2 − 5).
Câu 17:
 Xem đáp án
Xem đáp án
Lời giải
Với đoạn thẳng AB và góc α (0o < α < 180o) cho trước thì quỹ tích các điểm M thỏa mãn \[\widehat {AMB}\] = α là hai cung chứa góc α dựng trên đoạn AB.
Hai cung chứa góc α nói trên là hai cung tròn đối xứng nhau qua AB. Hai điểm A, B được coi là thuộc quỹ tích.
Câu 18:
 Xem đáp án
Xem đáp án
Lời giải

Gọi t là thời gian đi của ba xe.
Chọn mốc O tại A
Chiều Ox là chiều từ A đến C
• x1 = 50t
• x2 = 10 +30t
• x3 = 15 + 20t
Xe thứ hai ở chính giữa khi: \[{x_2} = \frac{{{x_1} + {x_3} & }}{2}\]
⇔ 2(10 + 30t) = 50t +15 +20t
⇔ t = 0,5 (h)
Quãng đường xe thứ hai đi được là:
s2 = v2 . t = 30 . 0,5 = 15 (km)
Vậy xe thứ hai đi được quãng đường là 15 km.
Câu 19:
 Xem đáp án
Xem đáp án
Lời giải
Ta có M ∈ Ox nên M(m; 0) và M = (–1 – m; 4).
Theo giả thiết
\[MN = 2\sqrt 5 \Leftrightarrow \]\[\left| {\overrightarrow {MN} } \right| = 2\sqrt 5 \Leftrightarrow \sqrt {{{\left( { - 1 - m} \right)}^2} + {4^2}} = 2\]
\[ \Leftrightarrow {\left( {1 + m} \right)^2} + 16 = 20 \Leftrightarrow {m^2} + 2m - 3 = 0\]
\[ \Leftrightarrow \left[ \begin{array}{l}m = 1 \Rightarrow M(1;\,\,0)\\m = - 3 \Rightarrow M( - 3;\,\,0)\end{array} \right.\].
Câu 20:
Phân tích đa thức sau thành nhân tử:
B = 2(x4 + y4 + z4) – (x2 + y2 + z2)2 – 2(x2 + y2 + z2)(x + y + z)2 + (x + y + z)4.
 Xem đáp án
Xem đáp án
Lời giải
Đặt x4 + y4 + z4 = a; x2 + y2 + z2 = b; x + y + z = c.
Khi đó 2(x4 + y4 + z4) – (x2 + y2 + z2)2 – 2(x2 + y2 + z2)(x + y + z)2 + (x + y + z)4
= 2a – b2 –2bc2 + c4
= 2a – 2b2 + b2 – 2bc2 + c4
= 2(a – b2) + (b + c2)2.
Ta có 2(a – b2) = 2[x4 + y4 + z4 – (x2 + y2 + z2)2]
= 2[x4 + y4 + z4 – x4 – y4 – z4 – 2x2y2 – 2y2z2 – 2z2x2]
= 2 . (–2)(x2y2 + y2z2 + z2x2)
= – 4(x2y2 + y2z2 + z2x2).
Lại có (b + c2)2 = [(x2 + y2 + z2) + (x + y + z)2]2
= [(x2 + y2 + z2) – (x2 + y2 + z2) – 2(xy + yz + zx)]2
= 4(xy + yz + zx)2
Suy ra 2(a – b2) + (b + c2)2
= – 4(x2y2 + y2z2 + z2x2) + 4(xy + yz + zx)2
= 8xyz(x + y + z).
Câu 21:
 Xem đáp án
Xem đáp án
Lời giải
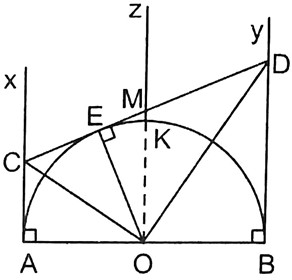
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
• OC là tia phân giác của \[\widehat {AOM}\];
• OD và tia phân giác của \[\widehat {BOM}\].
Khi đó, OC và OD là các tia phân giác của hai góc kề bù \[\widehat {AOM}\] và \[\widehat {BOM}\].
Do đó OC ⊥ OD.
Vậy \[\widehat {COD} = 90^\circ \] (đpcm)
b) Ta có: AC = CM, BD = DM nên AC . BD = CM . MD.
Xét ΔCOD vuông tại O, ta có:
CM . MD = OM2 = R2 (R là bán kính đường tròn O).
Vậy AC . BD = R2 (không đổi).
Câu 22:
Cho hai đường tròn (O; R) và (O'; R') tiếp xúc ngoài tại A (R > R'). Vẽ dây AM của đường tròn (O) và dây AN của đường tròn (O') sao cho AM ⊥ AN. Gọi BC là tiếp tuyến chung ngoài của hai đường tròn (O) và (O') với B thuộc (O) và C thuộc (O').
a) Chứng minh ba đường thẳng MN, BC và OO' đồng quy.
b) Xác định vị trí của M và N để tứ giác MNOO' có diện tích lớn nhất. Tính giá trị lớn nhất đó.
 Xem đáp án
Xem đáp án
Lời giải
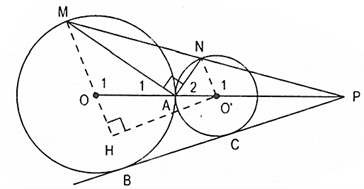
a) Ta có:
• \({\widehat O_1} = 180^\circ - 2{\widehat A_1}\)
• \({\widehat {O'}_1} = 2{\widehat A_2} = 2\left( {90^\circ - {{\widehat A}_1}} \right) = 180^\circ - 2{\widehat A_1}\)
Do đó: \({\widehat O_1} = {\widehat {O'}_1} \Rightarrow OM\;{\rm{//}}\;O'N\).
Gọi P là giao điểm của MN và OO'.
Ta có: \(\frac{{PO'}}{{PO}} = \frac{{O'N}}{{OM}} = \frac{{R'}}{R}\).
Gọi P' là giao điểm của BC và OO'.
Vì OB // O'C nên \(\frac{{P'O'}}{{P'O}} = \frac{{O'C}}{{OB}} = \frac{{R'}}{R}\).
Suy ra P' ≡ P.
b) Từ O' kẻ O'H ^ MO. Khi đó:
\({S_{OMNO'}} = \frac{{\left( {O'N + OM} \right).O'H}}{2} = \frac{{\left( {R' + R} \right).O'H}}{2}\)
\( \le \frac{{\left( {R' + R} \right).O'O}}{2} = \frac{{{{\left( {R' + R} \right)}^2}}}{2}\).
Dấu “=” xảy ra khi và chỉ khi O'H = O'O hay H ≡ O
Û O'O ^ MO hoặc O'O ^ NO'.
Vậy tứ giác MNO'O có diện tích lớn nhất là \(\frac{{{{\left( {R' + R} \right)}^2}}}{2}\) Û O'O ^ MO.
Câu 23:
 Xem đáp án
Xem đáp án
Lời giải
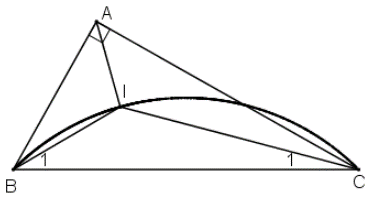
Dự đoán : Quỹ tích điểm I là cung chứa góc 135º dựng trên đoạn BC.
* Chứng minh :
Phần thuận : Chứng minh mọi điểm I thỏa mãn điều kiện trên đều thuộc cung chứa góc 135º dựng trên đoạn BC.
⇒ I thuộc cung chứa góc 135º dựng trên đoạn thẳng BC.
Phần đảo: Chứng minh mọi điểm I thuộc cung chứa góc 135º dựng trên đoạn BC, đều có tam giác ABC thỏa mãn điều kiện.
+ Lấy I trên cung chứa góc 135º dựng trên đoạn BC.
+ Kẻ tia Bx sao cho BI là phân giác của \(\widehat {ABC}\).
+ Kẻ tia Cy sao cho CI là phân giác của \[\widehat {ACB}\].
+ Bx cắt Cy tại A.
Khi đó I là giao điểm của hai đường phân giác trong tam giác ABC.
Vậy ΔABC vuông tại A thỏa mãn đề bài.
Kết luận: Quỹ tích điểm I là toàn bộ cung chứa góc 135º dựng trên đoạn BC (khác B và C).
Câu 24:
Cho ∆ABC vuông tại A, đường cao AH. Gọi AD là phân giác trong của ∆AHC.
a) Chứng minh ∆ BAD là tam giác cân;
b) Cho BC = 25 cm, HD = 6 cm. Tính AB.
 Xem đáp án
Xem đáp án
Lời giải
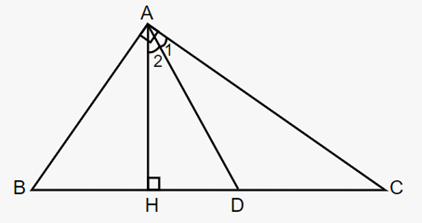
a) Ta có \[\widehat {BDA} = 90^\circ - {\widehat A_2}\] ; \[{\widehat A_1} = {\widehat A_2}\].
Suy ra \[\widehat {BAD} = \widehat {BDA}\].
Do đó ∆BAD cân tại B.
b) Ta có BH . BC = AB2
⇒ (x – 6) . 25 = x2 ⇒ x2 − 25x + 150 = 0
⇔ x = 10 hoặc x = 15.
Vậy AB = 10 cm hoặc AB = 15 cm.
Câu 25:
Cho a, b, c là các số thực không âm thỏa mãn a + b + c = 3.
Tìm giá trị lớn nhất của P = a2 + b2 + c2 + 3\[\sqrt {abc} \].
 Xem đáp án
Xem đáp án
Lời giải
Ta có \[P \le \sqrt {{a^2} + 2\sqrt a ab + 2{b^2}} + \sqrt {{b^2} + 2\sqrt 2 bc + 2{c^2}} + \sqrt {{c^2} + 2\sqrt 2 ca + 2{a^2}} \]
\[P \le \sqrt {{{\left( {a + \sqrt 2 b} \right)}^2}} + \sqrt {{{\left( {b + \sqrt 2 c} \right)}^2}} + \sqrt {{{\left( {c + \sqrt 2 a} \right)}^2}} \]
\[P \le {\left( {1 + \sqrt 2 } \right)^2}\left( {a + b + c} \right) = 1 + \sqrt 2 \]
Dấu "=" xảy ra khi (a; b; c) = (0; 0; 1) và các hoán vị.
Vậy giá trị lớn nhất của biểu thức P là \[1 + \sqrt 2 \] khi (a; b; c) = (0; 0; 1) và các hoán vị.
Câu 26:
 Xem đáp án
Xem đáp án
Lời giải
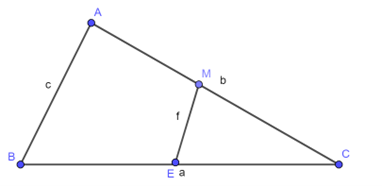
Ta có \[\overrightarrow {MN} = \overrightarrow {MC} + \overrightarrow {CN} = \frac{1}{2}\overrightarrow {BC} + \frac{{9 - x}}{9}\overrightarrow {CA} \]\[ = \frac{1}{2}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) + \frac{{x - 9}}{9}\overrightarrow {AC} = - \frac{1}{2}\overrightarrow {AB} + \left( { - \frac{1}{2} + \frac{x}{9}} \right)\overrightarrow {AC} \].
Câu 27:
Cho tam giác nhọn ABC có đường cao AH. Từ H kẻ HF vuông góc với AB (F ∈ AB) và kẻ HE ⊥ vói AC (E ∈ AC).
a) Chứng minh: \[\widehat {AFE} = \widehat {ACB}\].
b) Hai đường thẳng EF và BC cắt nhau tại M. Chứng minh ME . MF = MB . MC.
 Xem đáp án
Xem đáp án
Lời giải
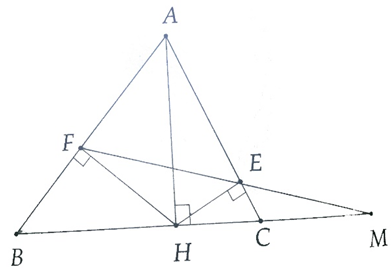
a) Xét (O) có ΔABC nội tiếp BC là đường kính.
Do đó ΔABC vuông tại A.
Xét ΔABC vuông tại A có AH là đường cao nên AH . BC = AB . AC.
Xét ∆MAB và ∆MCA có
\[\widehat M\] chung
\[\widehat {MAB} = \widehat {MCA}\] (cùng chắn ).
Do đó ∆MAB đồng dạng ∆MCA (g.g).
Suy ra \[\frac{{MA}}{{MC}} = \frac{{MB}}{{MA}}\].
Vậy MA2 = MB . MC.
Câu 28:
Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).
a) Chứng minh rằng: OA ⊥ BC.
b) Vẽ đường kính CD. Chứng minh rằng BD song song với AO.
c) Tính độ dài các cạnh của ∆ ABC; Biết OB = 2 cm, OA = 4 cm.
 Xem đáp án
Xem đáp án
Lời giải
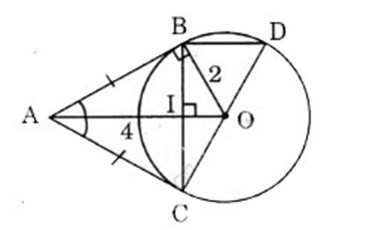
a) Vì AB, AC là các tiếp tuyến của (O) nên AB = AC nên ΔABC cân tại A.
Ta có AO là đường phân giác của góc \[\widehat {BAC}\] của tam giác cân ABC nên AO cũng là đường cao.
Suy ra OA ⊥ BC (tính chất của tam giác cân).
b) Gọi I là giao điểm của AO với BC.
Ta có ΔIBA = ΔICA (cạnh huyền - góc nhọn).
Suy ra IB = IC (hai cạnh tương ứng).
Trong ΔBCD có: IB = ID; OC = OD.
Suy ra OI là đường trung bình của ΔBCD.
Nên OI // BD hay AO// BD.
Vậy AO // BD (đpcm).
c) Vì AB là tiếp tuyến của (O) với B là tiếp điểm nên AB ⊥ OB và AB = AC.
Do đó ΔOAB vuông tại B.
Áp dụng định lí Py-ta-go vào tam giác vuông OAB, ta có:
AO2 = AB2 + BO2
⇒ AB2 = AO2 – BO2 = 42 – 22 = 12
⇒ AB = \[\sqrt {12} \] = \[2\sqrt 3 \] (cm)
Trong tam giác vuông OAB ta có
sin\[\widehat {OAB}\] = \[\frac{{OA}}{{OB}}\] = \[\frac{2}{4}\] = \[\frac{1}{2}\]
⇒ \[\widehat {OAB}\] = 30° ⇒ \[\widehat {BAC}\] = 2\[\widehat {OAB}\] = 2 . 30° = 60°
Xét ∆ABC cân tại A có \[\widehat A = 60^\circ \] nên ΔABC là tam giác đều.
Do đó AB = BC = CA = \[2\sqrt 3 \] (cm).
Câu 29:
Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AM, AN với đường tròn (M, N là các tiếp điểm).
a) Chứng minh rằng OA ⊥ MN.
b) Vẽ đường kính NC. Chứng minh rằng MC // AO.
c) Tính độ dài các cạnh của ∆AMN biết OM = 3 cm, OA = 5 cm.
 Xem đáp án
Xem đáp án
Lời giải
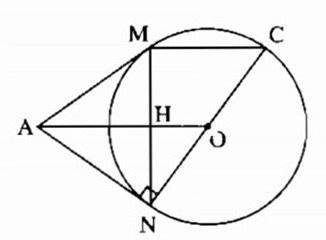
a) Ta có: AN = AM (tính chất tiếp tuyến)
Suy ra ∆AMN cân tại A
Mặt khác, OA là tia phân giác cũng là đường cao
Do đó OA ⊥ MN (đpcm).
b) Đặt H là giao điểm của MN và AO.
Ta có MH = HN (OA ⊥ MN nên H là trung điểm MN).
Mà CO = CN = R.
Suy ra OH là đường trung bình của ∆MNC.
Do đó OH // MC hay MC // OA (đpcm).
c) Ta có OM = ON = R nên ON = 3 cm.
Ta có: ON2 + AN2 = AO2 (theo định lý Py-ta-go)
Suy ra AN2 = AO2 – ON2 = 52 – 32 = 25 – 9 = 16
⇒ AN = \[\sqrt {16} \] = 4 (cm)
Ta có: AO.HN = AN.NO (hệ thức lượng trong tam giác vuông).
Suy ra 5HN = 4 . 3 = 12 ⇒ HN = \[\frac{{12}}{5}\] = 2,4 (cm).
Ta có MN = 2HN = 2 . 2,4 = 4,8 (vì H là trung điểm MN).
Vậy AM = AN = 4 cm; MN = 4,8 cm.
Câu 30:
 Xem đáp án
Xem đáp án
Lời giải
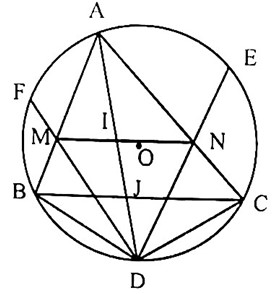
Gọi (Q) là đường thẳng Ơ-le, H là trực tâm, K là trung điểm AH, M là giao AH và BC.
Suy ra M, K, D ∈ (Q)
Gọi P là đầu thứ hai đường kính qua A.
Suy ra CP // BH (cùng ⊥ AC), BP // CH (cùng ⊥ AB)
Nên BPCH là hình bình hành
Do đó HP cắt BC tại trung điểm BC, tức HP đi qua D ⇒ OD là đường trung bình của ∆PAH ⇒ OD = \[\frac{{AH}}{2}\] = AK
⇒ AODK là hình bình hành ⇒ DK // AO ⇒ DD' trùng với DK
Do đó DK là đường kính của (Q), tức DD' đi qua tâm đường thẳng Euler
Vậy nên EE', FF' cũng đi qua tâm đường thẳng Euler.
Câu 31:
 Xem đáp án
Xem đáp án
Lời giải
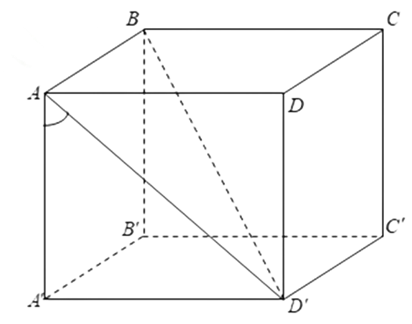
Ta có \[\left\{ \begin{array}{l}\left( {ABB'A'} \right) \cap \left( {D'AB} \right) = AB\\\left( {ABB'A'} \right) \bot AB\end{array} \right.\] nên góc giữa mặt phẳng (ABB’A’) là góc giữa AD’ và AA’ hay \[\widehat {A'AD}\] = 30°
Suy ra \[AA' = \frac{{A'D'}}{{\tan 30^\circ }} = a\sqrt 3 \]
Ta có \[{S_{ABCD}} = a.a = {a^2}\].
Vậy thể tích hình hộp đứng ABCD.A'B'C'D' là:
VABCD.A’B’C’D’ = AA’ . SABCD = \[{a^2}\,.\,a\sqrt 3 = {a^3}\sqrt 3 \] (đvtt).
Vậy thể tích hình hộp đứng ABCD.A'B'C'D' là \[{a^3}\sqrt 3 \] (đvtt).
Câu 32:
 Xem đáp án
Xem đáp án
Lời giải
Đặt A = sin6°.cos12°.cos24°.cos48°
Suy ra A. cos6° = sin6°.cos6°.cos12°.cos24°.cos48°
= \[\frac{1}{2}\]sin12°.cos12°.cos24°.cos48°
= \[\frac{1}{4}\]sin24°.cos24°.cos48° = \[\frac{1}{8}\]sin48°.cos48°
\[ = \frac{1}{{16}}sin96^\circ = \]\[\frac{1}{{16}}cos6^\circ \].
Do đó \[A = \frac{1}{{16}}\].
Câu 33:
Cho tam giác ABC cân tại A, đường phân giác trong của góc B cắt AC tại D và cho biết AB = 15cm, BC = 10cm. Khi đó AD = ?
 Xem đáp án
Xem đáp án
Lời giải
Đáp án đúng là: C
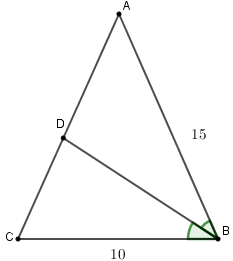
Vì BD là đường phân giác của \(\widehat {ABC}\) nên \(\frac{{AD}}{{DC}} = \frac{{AB}}{{BC}}\).
Suy ra \(\frac{{AD}}{{DC + AD}} = \frac{{AB}}{{BC + AB}}\) (theo tính chất dãy tỉ số bằng nhau)
Do đó \(\frac{{AD}}{{AC}} = \frac{{AB}}{{BC + AB}}\).
Mà tam giác ABC cân tại A nên AC = AB = 15 cm.
Câu 34:
Từ điểm A nằm ngoài đường tròn (O), vẽ tiếp tuyến AB đến (O) (B là tiếp điểm). Vẽ BE là đường kính của (O). Dựng đường cao BC của ∆OAB, tia BC cắt (O) tại D (D khác B).
a) Chừng minh AD là tiếp tuyến của (O) và OA // DE.
b) Gọi F là giao điểm của AE và (O) (F khác E). Chứng minh AE . AF = AC . AO.
c) Gọi G là giao điểm của BF và ED, H là giao điểm của AE và BD, I là giao điểm của AB và DE. Chứng minh GH // AB và AB = AI.
 Xem đáp án
Xem đáp án
Lời giải
a) Ta có: OB = OD (= R) nên ∆ODB cân tại O.
Mà OC là đường cao của ∆ODB.
Nên OC cũng là đường phân giác của ∆ODB.
⇒ \[\widehat {BOC} = \widehat {COD}\] hay \[\widehat {BOA} = \widehat {AOD}\].
Xét ∆ABO và ∆ADO có:
OB = OD (= R)
\[\widehat {BOA} = \widehat {AOD}\] (chứng minh trên)
Cạnh OA chung
Do đó ∆ABO = ∆ADO (c.g.c)
Suy ra \[\widehat {ABO} = \widehat {ADO} = 90^\circ \].
Do đó AD là tiếp tuyến của (O).
Ta có: \[\widehat {DEB} = \frac{1}{2}\] sđ (1)
Lại có: \[\widehat {BOD}\] = sđ
Mà \[\widehat {BOA}\] = \[\frac{1}{2}\]\[\widehat {BOD}\]
Nên \[\widehat {BOA}\] = \[\frac{1}{2}\] sđ (2)
Từ (1) và (2) suy ra \[\widehat {BOA} = \widehat {DEO}\].
Mà hai góc này nằm ở vị trí đồng vị nên OA // DE.
b) Vì F thuộc đường tròn đường kính BE nên \[\widehat {BFE} = 90^\circ \]
Xét ∆ABE vuông tại B có: BF là đường cao
Suy ra AE . AF = AB2
Chứng minh tương tự, ta có: AC . AO = AD2.
Mà AB = AD (tính chất hai tiếp tuyến cắt nhau)
Do đó AB2 = AD2
Suy ra: AE . AF = AC.AO.
c) Vì D thuộc đường tròn đường kính BE nên \[\widehat {BDE} = 90^\circ \].
Ta có: BD là đường cao của ∆BGE; EF là đường cao của ∆BGE.
Mà BD, EF cắt nhau tại H.
Do đó H là trực tâm của ∆BGE.
Suy ra: GH ⊥ BE; AB ⊥ BE
Nên GH // AB.
Xét ∆BIE có: BO = EO (= R); AO // EI (AO // DE).
Do đó AB = AI.
Câu 35:
Cho ba điểm A(– 4; 0), B(0; 3) C(2; 1).
a) Xác định tọa độ \[\overrightarrow u = 2\overrightarrow {AC} \;--\overrightarrow {AB} \].
b) Tìm điểm M sao cho MA + 2MB + 3MC = 0.
 Xem đáp án
Xem đáp án
Lời giải
a) Ta có \[\overrightarrow {AB} = \left( {4;\,\,3} \right);\,\,\overrightarrow {AC} = \left( {6;\,\,1} \right)\]
Suy ra \[2\overrightarrow {AC} = \left( {12;\,\,2} \right)\]
Do đó \[\overrightarrow u = \left( {12 - 4;\,\,2 - 3} \right) = \left( {8;\,\, - 1} \right)\].
b) Ta có \[M\left( {x;\,\,y} \right) \Rightarrow \left\{ \begin{array}{l}\overrightarrow {MA} = \left( { - \,4 - x;\,\, - y} \right)\\\overrightarrow {MB} = \left( { - \,x;\,\,3 - y} \right)\\\overrightarrow {MC} = \left( {2 - x;\,\,1 - y} \right)\end{array} \right.\]
Khi đó \[\overrightarrow {MA} + 2\overrightarrow {MB} + 3\overrightarrow {MC} = \left( {2 - 6x;\,\,9 - 6y} \right)\]
\[ \Rightarrow \left\{ \begin{array}{l}2 - 6x = 0\\9 - 6y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{1}{3}\\y = \frac{3}{2}\end{array} \right.\].
Do đó \[M\left( {\frac{1}{3};\,\,\frac{3}{2}} \right)\].
Câu 36:
Cho ∆ABC cân tại A, trung tuyến AM. Gọi I là trung điểm của AC, K là điểm đối xứng của điểm M qua điểm I.
a) Tứ giác AMCK là hình gì?
b) Tứ giác AKMB là hình gì?
c) Có trường hợp nào của ∆ABC để tứ giác AKMB là hình thoi không? Vì sao?
 Xem đáp án
Xem đáp án
Lời giải
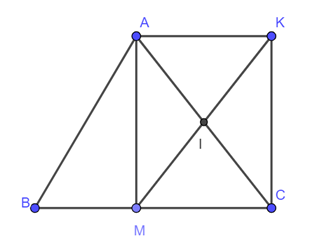
a) Áp dụng tính chất của ∆ cân cho DABC ta có: AM ⊥ MC và BM = MC
Vì I là trung điểm của AC và K đối xứng với M qua I nên tứ giác AMCK là hình bình hành.
Lại có MK = AC (= 2MI).
Do đó, tứ giác AMCK là hình chữ nhật.
b) Vì tứ giác AMCK là hình chữ nhật (theo câu a).
Do đó AK // MC và AK = MC = MB.
Vậy tứ giác AKMB là hình bình hành.
c) Nếu tứ giác AKMB là hình thoi thì BA = AK = KM = MB.
Vì DMBA cân tại B nên \[\widehat {BAM} = \widehat {AMB}\] = 90° (vô lí).
Vậy không có trường hợp nào của DABC để AKMB là hình thoi.
Câu 37:
 Xem đáp án
Xem đáp án
Lời giải
• Với x = 0, ta có: P = 0
• Với x ≠ 0, ta có:
\[P = \frac{{{x^2}}}{{{x^4} + {x^2} + 1}} = \frac{1}{{{x^2} + \frac{1}{{{x^2}}} + 1}} \le \frac{1}{{2 + 1}} = \frac{1}{3}\]
Vậy giá trị lớn nhất của biểu thức P bằng \[\frac{1}{3}\] khi x = ± 1.
Câu 38:
 Xem đáp án
Xem đáp án
Lời giải
Số nguyên tố là số tự nhiên lớn hơn 1 không phải là tích của hai số tự nhiên nhỏ hơn.
Nói cách khác: Số nguyên tố là những số chỉ có đúng hai ước số là 1 và chính nó. Các số tự nhiên lớn hơn 1 không phải là số nguyên tố được gọi là hợp số.
Câu 39:
 Xem đáp án
Xem đáp án
Lời giải
• Các số nguyên tố là: 79 và 61. Vì 79 chỉ có 2 ước là 1 và 79 và 61 chỉ có 2 ước là 1 và 61.
• Các hợp số là: 77 và 121. Vì 77 ⋮ 7 và 121 ⋮ 11 nên 77 và 121 có nhiều hơn 2 ước là 1 và chính nó.
Câu 40:
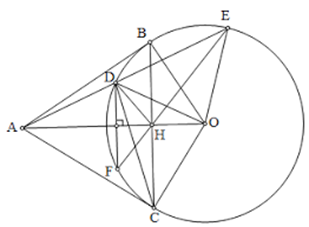
Cho đường tròn tâm O, đường kính AB và điểm C thuộc đường tròn sao cho AC > BC. Qua O vẽ đường thẳng vuông góc với dây AC ở H. Kẻ tiếp tuyến tại A của đường tròn cắt tia OH ở D. BD cắt đường tròn tâm O ở E.
a) Chứng minh HA = HC.
b) Biết \[\widehat {DCO} = 90^\circ \]. Chứng minh OH . DO = DE . DB.
c) Trên tia đối của EA lấy F sao cho E là trung điểm AF. Từ F vẽ đường thẳng AD vuông góc ở K; KF cắt BC ở M. Chứng minh MK = MF.
 Xem đáp án
Xem đáp án
Lời giải
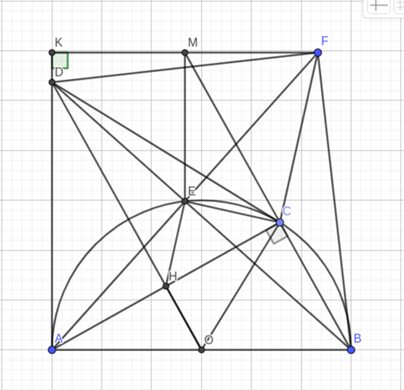
a) Vì A, C ∈ (O); OH ⊥ AC ⇒ H là trung điểm của AC ⇒ HA = HC
Do AH = HC, DO ⊥ AC ⇒ DO là đường trung trực của AC
b) Vì \[\widehat {DCO}\] = 90°, CH ⊥ DO ⇒ DC2 = DH . DO
Mà ∆DCE ᔕ ∆DBC (g.g).
Suy ra DE . DB = DC2
Do đó DH . DO = DE . DB.
c) Ta có E là trung điểm AF, H là trung điểm AC là đường trung bình.
Mà tứ giác ADEH nội tiếp do \[\widehat {DEA} = \widehat {DHA} = 90^\circ \].
Lại có \[\widehat {FED} = \widehat {CBA} = \widehat {DOA}\] ⇒ \[\widehat {DAO} = \widehat {FCE}\] = 90°
Mặt khác: FK // AB ⇒ \[\widehat {FMC} = \widehat {MBA} = \widehat {FEC}\]
\[\widehat {EMF} + \widehat {EFC}\] = 90° ⇒ \[\widehat {EFM}\] = 90° ⇒ EM // AK.
Do đó M là trung điểm của KF (E là trung điểm của AC).
Câu 41:
 Xem đáp án
Xem đáp án
Lời giải
Không gian mẫu: 36.
Số biến cố thỏa mãn: (11), (22), (33), (44), (55), (66) tổng cộng 6 biến cố.
Xác suất: \[P = \frac{6}{{36}} = \frac{1}{6}\].
Câu 42:
 Xem đáp án
Xem đáp án
Lời giải
Gọi T là biến cố "Số chấm xuất hiện chia hết cho 2".
Khi đó, không gian mẫu: Ω = {1; 2; 3; 4; 5; 6} = 6.
Biến cố của T là số chấm chia hết cho 2: ΩT = {2; 4; 6} = 3.
Vậy xác suất của biến cố T là: P(T) = \[\frac{{{\Omega _T}}}{\Omega } = \frac{1}{2}\].
Câu 43:
Cho ∆ ABC vuông tại A có AB = 3 cm, AC = 4 cm.
a) Giải ∆ABC.
b) Gọi I là trung điểm của BC, vẽ AH ⊥ BC. Tính AH, AI.
c) Qua A kẻ đường thẳng vuông góc với AI. Đường thẳng vuông góc với BC tại B cắt xy tại điểm M, đường thẳng vuông góc với BC tại C cắt xy tại điểm N. Chứng minh \[MB\,\,.\,NC = \frac{{B{C^2}}}{4}\].
 Xem đáp án
Xem đáp án
Lời giải
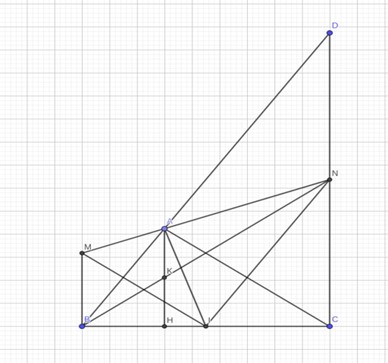
Áp dụng định lý Py-ta-go vào ∆ABC vuông tại A, ta có:
BC = \[\sqrt {A{B^2} + A{C^2}} = 5\] (cm)
sin\[\widehat B\] = \[\frac{{AB}}{{AC}} = \frac{4}{5}\] ⇒ \[\widehat B \approx 53^\circ \]
\[\widehat C = 90^\circ - \widehat B = 37^\circ \]
b) Vì AI là trung tuyến ứng ch BC nên AI = \[\frac{1}{2}\]BC = 2,5 (cm)
AH. BC = AB . AC ⇒ AH = \[\frac{{AB.AC}}{{BC}} = \frac{{12}}{5}\](cm)
c) Xét ∆AMI và ∆BMI có:
IA = IB
\[\widehat {IAM} = \widehat {IAM} = 90^\circ \]
IM chung
Do đó ∆AMI = ∆BMI (cạnh huyền – góc vuông)
Suy ra \[\left\{ \begin{array}{l}MA = MB\\\widehat {AIM} = \widehat {BIM}\end{array} \right.\] (các cạnh và các góc tương ứng).
Do đó IN là phân giác của \[\widehat {AIC}\].
Do \[\widehat {AIB} + \widehat {AIC}\]= 180° nên IM ⊥ IN.
Suy ra ∆IMN vuông tại I.
Mà IA ⊥ MN
Do đó MB . NC = AM . AN = IA2 = \[{\left( {\frac{{BC}}{2}} \right)^2} = \frac{{B{C^2}}}{4}\]
Câu 44:
 Xem đáp án
Xem đáp án
Lời giải
Số nhỏ nhất có 4 chữ số khác nhau là 1023.
Gọi số cần tìm là a.
Ta có: a : 6 = 1023
⇒ a = 6 . 1023 = 6138
Vậy số nhỏ nhất có bốn chữ số khác nhau chia hết cho 6 là 6138.
Câu 45:
 Xem đáp án
Xem đáp án
Lời giải
Số nhỏ nhất có 4 chữ số chia hết cho 6 là 1 002.
Số lớn nhất có 4 chữ số chia hết cho 6 là 9 002.
Câu 46:
Cho hình bình hành ABCD có BC = 2AB và \[\widehat A = 60^\circ \]. Gọi E, F theo thứ tự là trung điểm của BC và AD.
a) Tứ giác ECDF là hình gì? Vì sao?
b) Tam giác DEC là tam giác gì? Vì sao?
c) Tính số đo\[\widehat {AED}\]?
 Xem đáp án
Xem đáp án
Lời giải
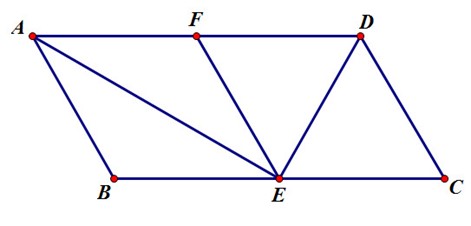
a) Ta có \[\left\{ \begin{array}{l}BC = 2AD = 2AB = 2AE = 2FD\\BC = 2BE = 2EC\end{array} \right.\]
Suy ra AB = BE = EC = CD = FD = AF
Tứ giác ECFD có \[\left\{ \begin{array}{l}FD//EC\\FD = EC\end{array} \right.\]
Do đó tứ giác ECFD là hình bình hành.
b) ∆ DEC có: \[\left\{ \begin{array}{l}DC = EC\\\widehat A = \widehat C = 60^\circ \end{array} \right.\] ⇒ ∆ DEC là ∆ đều
c) Ta có: tứ giác ABEF là hình bình hành nên AB // FE ⇒ \[\widehat {AEF} = \widehat {EAB}\] (1)
• Xét ∆AFE có AF = FE nên ∆AFE là tam giác cân.
Do đó \[\widehat {FAE} = \widehat {FEA}\] (2)
Từ (1) và (2) suy ra \[\widehat {BAE} = \widehat {EAF} = \widehat {FEA} = \frac{{60^\circ }}{2} = 30^\circ \].
• Xét ∆FED có \[\left\{ \begin{array}{l}FD = DC = DE\\\widehat {FDE} = 60^\circ \end{array} \right.\] nên ∆FED là tam giác đều.
Suy ra \[\widehat {FDE} = \widehat {DEF} = \widehat {EFD} = \frac{{180^\circ }}{3} = 60^\circ \].
Ta có \[\widehat {AED} = \widehat {AEF} + \widehat {FED} = 30^\circ + 60^\circ = 90^\circ \]
Câu 47:
Cho số thực x, y thỏa mãn: \[x - \sqrt {x + 6} = \sqrt {y + 6} - y\].
Tìm giá trị lớn nhất và giá trị nhỏ nhất của P = x + y.
 Xem đáp án
Xem đáp án
Lời giải
• Ta có x + y = \[\sqrt {x + 6} + \sqrt {x + 6} \] ≥ 0 ⇒ x + y ≥ 0
\[x + y = \sqrt {x + 6} + \sqrt {y + 6} \le \sqrt {2\left( {x + y + 12} \right)} \]
\[ \Rightarrow {\left( {x + y} \right)^2} \le 2\left( {x + y + 12} \right)\]
\[ \Rightarrow (x + y + 4)(x + y - 6) \le 0\]
x + y ≤6 (do x + y + 4 > 0)
Do đó Pmax = 6 khi x = y = 3
• Lại có \[x + y = \sqrt {x + 6} + \sqrt {y + 6} \]
\[ \Rightarrow {(x + y)^2} = x + y + 12 + 2\sqrt {(x + 6)(y + 6)} \ge x + y + 12\]
\[ \Rightarrow {(x + y)^2} - (x + y) - 12 \ge 0\]
\[ \Rightarrow (x + y + 3)(x + y - 4) \ge 0\]
\[ \Rightarrow x + y - 4 \ge 0\]
\[ \Rightarrow x + y \ge 4\]
Pmin = 4 khi (x; y) = (–6; 10) và hoán vị.
Vậy giá trị lớn nhất của biểu thức P bằng 6 khi x = y = 3 và giá trị nhỏ nhất bằng 4 khi (x; y) = (–6; 10) và hoán vị.
Câu 48:
Cho tứ giác ABCD. Gọi O là giao điểm của hai đường chéo (không vuông góc), I và K lần lượt là trung điểm của BC và CD. Gọi M và N theo thứ tự là điểm đối xứng của điểm O qua tâm I và K.
a) Chứng minh rằng tứ giác BMND là hình bình hành.
b) Với điều kiện nào của hai đường chéo AC và BD thì tứ giác BMND là hình chữ nhật?
c) Chứng minh ba điểm M, C, N thẳng hàng.
 Xem đáp án
Xem đáp án
Lời giải
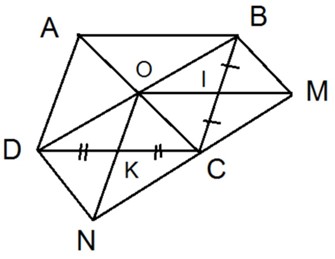
a) Ta có \[\left\{ \begin{array}{l}BH = HC\\MH = HO\end{array} \right.\]
Suy ra tứ giác BMND là hình bình hành
Do đó \[\left\{ \begin{array}{l}BM\parallel OC\\BM = OC\end{array} \right.\] (1)
Tương tự, tứ giác OCND là hình bình hành.
Suy ra \[\left\{ \begin{array}{l}DN\parallel OC\\DN = OC\end{array} \right.\] (2)
Từ (1) và (2) suy ra \[\left\{ \begin{array}{l}BM\parallel DN\\BM = OC = DN\end{array} \right.\]
Do đó tứ giác BMND là hình bình hành.
b) Ta có BMND là hình bình hành (câu a) trở thành hình chữ nhật thì BM // AC.
Vậy để BMND là hình chữ nhật thì BM // AC
c) Vì BMCO là hình bình hành nên MC // BD (3)
Và BMND là hình bình hành nên MN // BD (4)
Từ (3) và (4) suy ra M, N, C thẳng hàng (theo tiên đề Ơ–clit).Câu 49:
Cho tam giác ABC cân tại A có đường cao AD, O là trung điểm AC, điểm E đối xứng với điểm D qua điểm O.
a) Chứng minh tứ giác AECD là hình chữ nhật.
b) Gọi I là trung điểm AD, Chứng minh I là trung điểm BE.
 Xem đáp án
Xem đáp án
Lời giải:
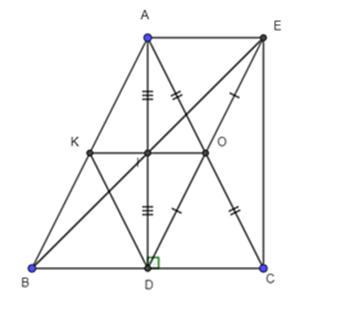
a) Vì O là trung điểm AC nên O là trung điểm của DE (E đối D qua O).
Suy ra AECD là hình bình hành (định nghĩa hình bình hành).
Mà \[\widehat {ADC}\] = 90° (AD ⊥ BC).
Do đó AECD là hình chữ nhật.
b) Vì AECD là hình chữ nhật (chứng minh trên).
Nên AE = CD và AE // CD (tính chất hình bình hành).
Mà DC = BD (D trung điểm BC do AD ⊥ BC, ΔABC cân tại A).
Do đó: AE // BD (B ∈ CD), AE = BD.
Suy ra AEDB là hình bình hành (định nghĩa hình bình hành)
Mà I là trung điểm AD nên I là trung điểm BE (tính chất hình bình hành).Câu 50:
 Xem đáp án
Xem đáp án
Lời giải
Số thập phân có 1 chữ số ở phần thập phân lớn hơn 8 và nhở hơn 10 là 8,1; 8,2; 8,3; ...; 9,9 có số số là: 99 – 81 + 1 = 19 (số).
Câu 51:
 Xem đáp án
Xem đáp án
Lời giải
Các số thập phân sẽ bắt đầu từ 12,51 đến 13,39.
Từ 12,51 đến 13 ta sẽ loại trừ :12,6; 12,7; 12,8; 12,9; 13.
Vậy sẽ có dãy số sau: 12,51; 12,52; ...; 12,59; 12,61;...; 12,99.
Từ 12,51 đến 12,59 có 9 số.
Vậy từ 12,51 đến 12,99 có số số là:
(9 – 5 + 1) . 9 = 45 (số).
Từ 13,01 đến 13,39 ta làm tương tự
(3 – 0 + 1) . 9 = 36 (số).
Vậy có số số thập phân thỏa mãn là: 45 + 36 = 81 (số).
Câu 52:
 Xem đáp án
Xem đáp án
Lời giải
Ta có \[sin\left( {2x + 20^\circ } \right) = \frac{{ - \sqrt 3 }}{2}\]
\[ \Leftrightarrow \sin (2x + 20^\circ ) = \sin ( - 60^\circ )\]
\[ \Leftrightarrow \left[ \begin{array}{l}2x + 20^\circ = - 60^\circ + k\,.\,360^\circ \\2x + 20^\circ = 180^\circ + 60^\circ + k\,.\,360^\circ \end{array} \right.\,\,(k \in \mathbb{Z})\]
\[ \Leftrightarrow \left[ \begin{array}{l}2x = - 80^\circ + k\,.\,360^\circ \\2x = 220^\circ + k\,.\,360^\circ \end{array} \right.\,\,(k \in \mathbb{Z})\]
\[ \Leftrightarrow \left[ \begin{array}{l}x = - 40^\circ + k\,.\,180^\circ \\x = 110^\circ + k\,.\,180^\circ \end{array} \right.\,\,(k \in \mathbb{Z})\]
Câu 53:
 Xem đáp án
Xem đáp án
Lời giải:
Hệ số tự do là số hạng không chứa biến.
Giá trị của đa thức f(x) tại x = a được kí hiệu là f(a) có được bằng cách thay x = a vào đa thức f(x) rồi thu gọn lại.
Câu 54:
 Xem đáp án
Xem đáp án
Lời giải
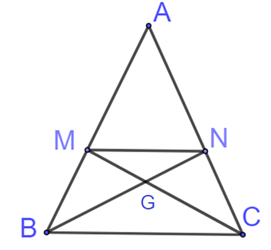
Gọi G là giao điểm của hai đường trung tuyến BM và CN.
Khi đó, G là trọng tâm tam giác ABC.
Áp dụng công thức đường trung tuyến:
• \[B{M^2} = \frac{{{c^2} + {a^2}}}{2} - \frac{{{b^2}}}{4}\]
• \[C{N^2} = \frac{{{a^2} + {b^2}}}{2} - \frac{{{c^2}}}{4}\]
• \[B{G^2} = \frac{4}{9}B{M^2} = \frac{2}{9}({c^2} + {a^2}) - 19{b^2}\]
• \[N{G^2} = \frac{1}{9}C{N^2} = \frac{1}{{18}}({a^2} + {b^2}) - \frac{1}{{36}}{c^2}\]
Theo công thức Py-ta-go, ta có: BN2 = BG2 + NG2
Áp dụng công thức cos, ta có:
\[\frac{{{c^2}}}{4} = \frac{2}{9}({c^2} + {a^2}) - \frac{1}{9}{b^2} + \frac{1}{{18}}({a^2} + {b^2}) - \frac{1}{{36}}{c^2} = 45\]
\[{a^2} = {b^2} + {c^2} - 2bc\cos A = {b^2} + {c^2} - \sqrt 3 bc\].
Diện tích tam giác ABC là:
\[{S_{ABC}} = \frac{1}{2}bc.sin\widehat A = \frac{1}{2}.12\sqrt 3 .sin30 = 3\sqrt 3 \] (đvdt).
Câu 55:
Cho ∆ ABC, M là trung điểm của BC, N là trung điểm của AC. lấy điểm E đối xứng với điểm M qua điểm N. Chứng minh:
a) Tứ giác AECM là hình bình hành.
b) Tứ giác AEMB là hình bình hình.
c) Tứ giác AECB là hình thang.
d) Tìm điều kiện của ∆ABC để hình bình hành AECM là hình chữ nhật.
 Xem đáp án
Xem đáp án
Lời giải
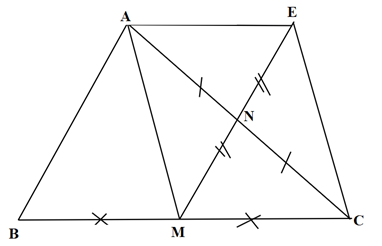
Tứ giác AECM có 2 đường chéo AC và EM cắt nhau tại trung điểm mỗi đường ⇒ Tứ giác AECM là hình bình hành
b) Do tứ giác AECM là hình bình hành ⇒ AE // CM
⇒ AE = CM mà CM = BM (M là trung điểm BC)
⇒ AE = BM
+) AE // CM mà M ∈ BC ⇒ BC // AE và BM // AE
+) Tứ giác AEMB có:
AE = BM
AE // BM
⇒ Tứ giác AEMB là hình bình hành
c) Tứ giác AECB có AE // BC ⇒ Tứ giác AECB là hình thang
d) Để hình bình hành AECM là hình chữ nhật
Thì \[\widehat {AMC}\] = 90° ⇒ AM là đường cao ΔABC
Mà AM cũng là đường trung tuyến
⇒ ΔABC cân tại A
Vậy để hình bình hành AECM là hình chữ nhật thì ΔABC cân ở A
Câu 56:
Trong mặt phẳng tọa độ Oxy cho parabol (P): y = \[ - \frac{1}{2}\]x2 và đường thẳng (d) y = mx + m – 3(với m là tham số).
a) Khi m = –1, tìm tọa độ giao điểm của đường thẳng (d) và parabol (P).
b) Tìm m để đường thẳng (d) và parabol (P)cắt nhau tại 2 điểm phân biệt có hoành độ x1, x2 thỏa mãn hệ thức x12 + x22 = 14.
 Xem đáp án
Xem đáp án
Lời giải
a) Phương trình hoành độ giao điểm:
\[ - \frac{1}{2}{x^2} = mx + m - 3 \Leftrightarrow {x^2} + 2mx + 2m - 6 = 0\] (1)
Khi m = −1, phương trình (1) trở thành:
\[{x^2} - 2x - 8 = 0 \Rightarrow \left[ \begin{array}{l}x = 4 \Rightarrow y = - 8\\x = - 2 \Rightarrow y = - 2\end{array} \right.\]
Vậy (d) cắt (P) tại 2 điểm có tọa độ là (4; –8); (–2; 2)
b) Ta có \[\Delta \prime = {m^2} - 2m + 6 = {(m + 1)^2} + 5 > 0;\forall m\].
Do đó m = −1 có 2 nghiệm phân biệt với mọi m.
Hay (d) cắt (P) tại hai điểm phân biệt với mọi m.
Theo hệ thức Vi-et: \[\left\{ \begin{array}{l}{x_1} + {x_2} = - 2m\\{x_1}{x_2} = 2m - 6\end{array} \right.\]
\[x_1^2 + x_2^2 = 14 \Leftrightarrow {({x_1} + {x_2})^2} - 2{x_1}{x_2} = 14\]
\[ \Leftrightarrow 4{m^2} - 2(2m - 6) = 14\]
\[ \Leftrightarrow 4{m^2} - 4m - 2 = 0 \Rightarrow m = \frac{{1 \pm \sqrt 3 }}{2}\].
