Cho hình vẽ dưới đây.
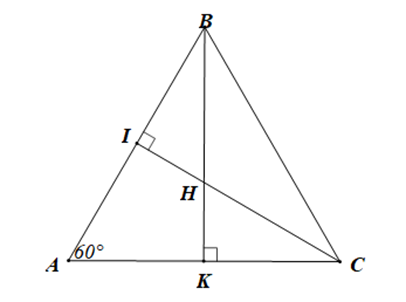
Tam giác BHC là tam giác gì?
A. Tam giác tù;
B. Tam giác vuông;
C. Tam giác nhọn;
D. Tam giác đều.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
Tam giác AIC vuông tại I \(\left( {\widehat I = 90^\circ } \right)\) nên \(\widehat A + \widehat {ACI} = 90^\circ \) (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra \(\widehat A = 90^\circ - \widehat {ACI}\) (1)
Tam giác CHK vuông tại K \(\left( {\widehat K = 90^\circ } \right)\) nên \(\widehat {CHK} + \widehat {KCH} = 90^\circ \) (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra \(\widehat {CHK} = 90^\circ - \widehat {KCH}\) (2)
Mà \(\widehat {ACI}\) chính là góc \(\widehat {KCH}\) (3)
Từ (1), (2) và (3) ta có: \(\widehat {CHK} = \widehat A = 60^\circ \)
Lại có \(\widehat {CHK}\) và \(\widehat {BHC}\) là hai góc kề bù nên \(\widehat {CHK} + \widehat {BHC} = 180^\circ \) (tính chất hai góc kề bù)
Suy ra \(\widehat {BHC} = 180^\circ - \widehat {CHK}\)
Do đó \(\widehat {BHC} = 180^\circ - 60^\circ = 120^\circ > 90^\circ \)
Khi đó góc BHC là góc tù
Vậy tam giác BHC là tam giác tù.
Cho hình vẽ:
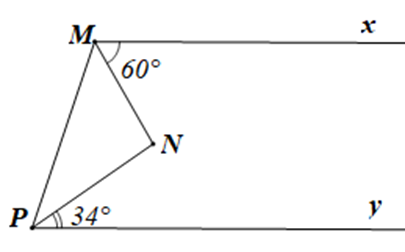
Biết Mx // Py, \(\widehat {xMN} = 60^\circ \) và \[\widehat {NPy} = 34^\circ .\] Tính số đo góc MNP và tam giác MNP là tam giác gì?
Cho tam giác ABC như hình vẽ có \(\widehat {ADC} = 60^\circ .\)
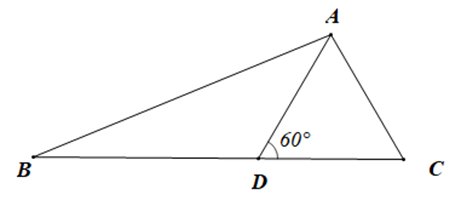
Tam giác ABD là tam giác gì?
Cho hình vẽ biết \(\widehat {ABC} = 50^\circ ,\widehat {ACB} = 40^\circ \) và \(\widehat {BAE} = \widehat {AED}.\)
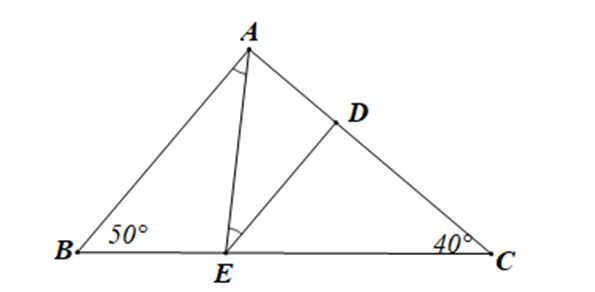
Tam giác CDE là tam giác gì?
Cho tam giác ABC có \(\widehat B = 35^\circ ,\widehat C = 65^\circ .\) Tia phân giác góc A cắt cạnh BC tại D.
Tam giác ADC là tam giác gì?
Cho tam giác ABC như hình vẽ:
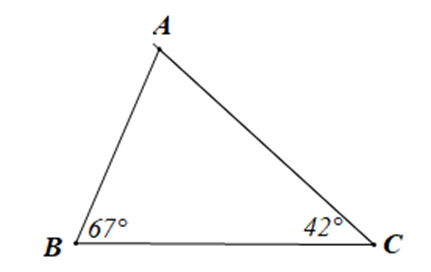
Tính số đo góc A và cho biết tam giác ABC là tam gác gì?
Cho tam giác ABC vuông tại A. Lấy điểm K nằm trên cạnh AC. Lấy điểm E nằm trên cạnh BK. Tam giác BEC là tam giác gì?
Cho hình vẽ như sau:
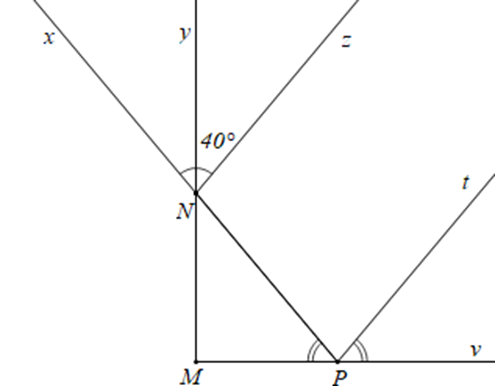
Biết tia Ny là tia phân giác của \(\widehat {xNz},\widehat {yNz} = 40^\circ ,\widehat {NPM} = \widehat {tPv}\) và Nz // Pt. Số đo của \(\widehat {NPM}\) là bao nhiêu và tam giác MNP là tam giác gì?