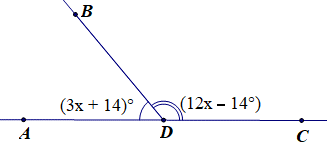
Tìm giá trị của x trong hình sau:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
Ta có \(\widehat {{\rm{ADB}}} + \widehat {BDC} = 180^\circ \)(hai góc kề bù)
Hay (3x + 14)° + (12x – 14)° = 180°
Suy ra (3x + 14 + 12x – 14)° = 180°
Do đó (15x)° = 180°
Suy ra 15x = 180
Nên x = 12
Vậy x = 12.
Ta chọn phương án B.
Cho hai góc \(\widehat {\rm{A}}\)và \(\widehat {\rm{B}}\) là hai góc bù nhau, biết rằng \(\widehat {\rm{A}} = 72^\circ \).Chọn khẳng định đúng
Cho ba đường thẳng xy, zt, mn cắt nhau tại O sao \(\widehat {{\rm{nOy}}} = 120^\circ \) và \(\widehat {{\rm{zOm}}} = 2\widehat {{\rm{xOz}}}\). Số đo góc đối đỉnh của \(\widehat {{\rm{zOm}}}\) bằng
Cho ba đường thẳng xy, zt, mn cắt nhau tại O sao cho \(\widehat {{\rm{zOm}}} = 58^\circ \)và \(\widehat {{\rm{yOt}}} = 35^\circ \) (như hình vẽ).
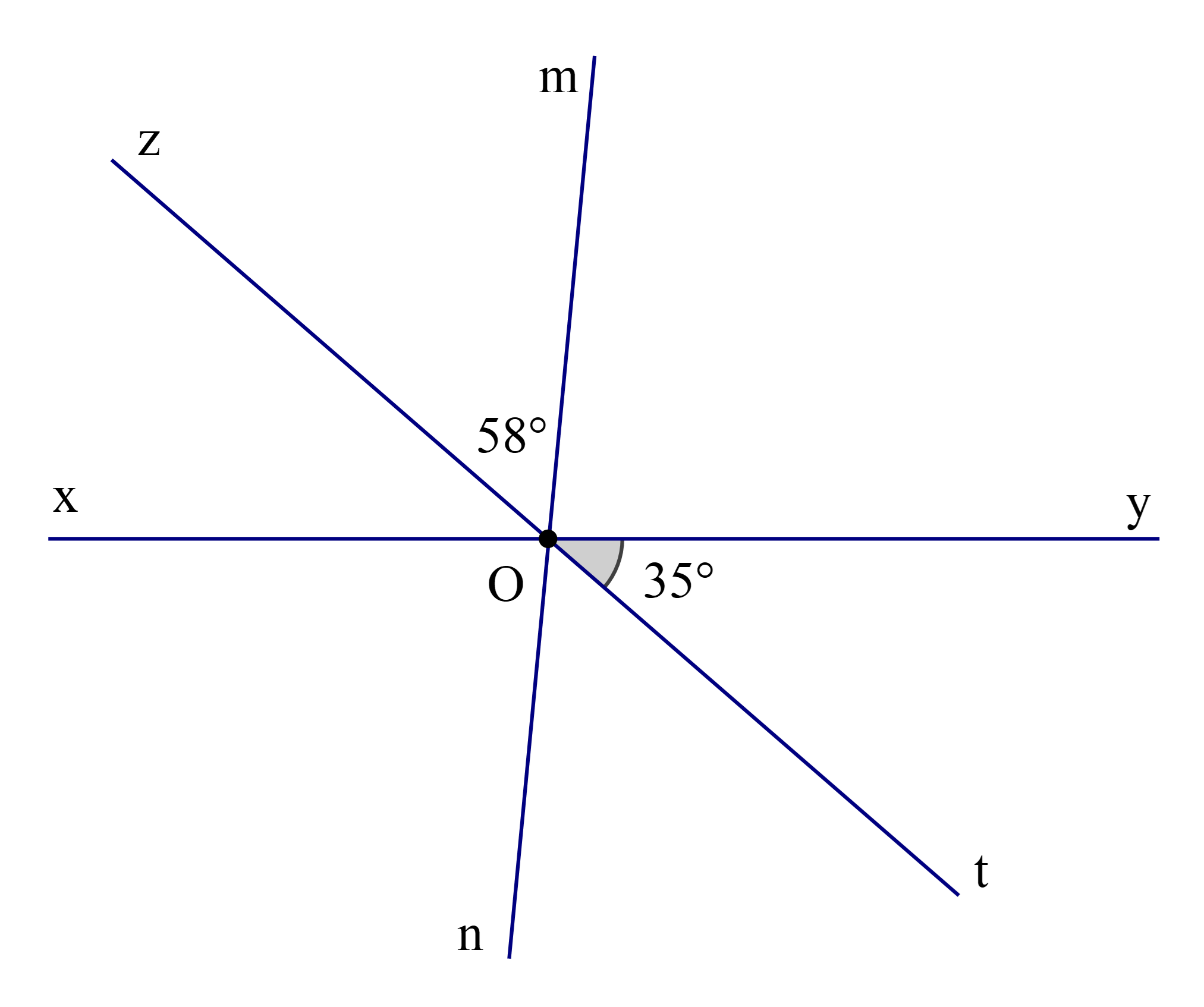
Số đo \(\widehat {{\rm{xOn}}}\) là:
Hai đường thẳng AB và EF cắt nhau tại O. Kẻ tia ON nằm giữa hai tia OB và OE sao cho \(\widehat {{\rm{EON}}} = \widehat {{\rm{NOB}}}\). Gọi OM là tia đối của tia ON. Chọn khẳng định đúng:
