Cho hai dao động điều hòa cùng phương, cùng tần số \({x_1} = {A_1}\cos \left( {\omega t + {\varphi _1}} \right)\) và \({x_2} = {A_2}\cos \left( {\omega t + {\varphi _2}} \right)\). Biên độ dao động tổng hợp của hai dao động trên có giá trị
B. \(A = A = \sqrt {A_1^2 + A_2^2 - 2{A_1}{A_2}\cos \frac{{{\varphi _1} + {\varphi _2}}}{2}} \)
D. \(A = \sqrt {A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \left( {{\varphi _2} - {\varphi _1}} \right)} \)
Giải bởi Vietjack
Chọn D
Trong quá trình giao thoa sóng, gọi \(\Delta \varphi \) là độ lệch pha của hai sóng thành phần, với \(n = 0,1\), \(2,3 \ldots \) thì biên độ dao động tổng hợp tại \(M\) trong miền giao thoa đạt giá trị nhỏ nhất khi:
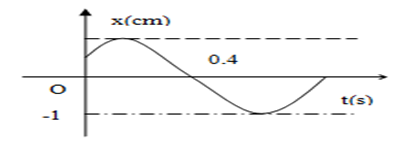
Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của li độ x vào thời gian t của một vật dao động điều hòa. Biên độ dao động của vật là
Khi xảy ra hiện tượng giao thoa sóng nước với hai nguồn kết hợp cùng pha \(A,B\). Những điểm trên mặt nước nằm trên đường trung trực của \(AB\) sẽ
Hai nguồn sóng kết hợp tại \({S_1}\) và \({S_2}\) dao động theo phương trình \({u_1} = {u_2} = A\cos \omega t\). Giả sử khi truyền đi biên độ sóng không đổi. Một điểm \(M\) cách \({S_1}\) và \({S_2}\) lần lượt là \({d_1}\) và \({d_2}\). Biên độ dao động tổng hợp tại \(M\) là
Trong dao động điều hòa với tần số góc \(\omega \) và biên độ \(A\), giá trị cực tiểu của vận tốc là
Tại một nơi có hai con lắc đơn dao động với biên độ nhỏ. Trong cùng một khoảng thời gian, con lắc thứ nhất thực hiện được 5 dao động toàn phần, con lắc thứ hai thực hiện được 4 dao động toàn phần. Tổng chiều dài hai con lắc là \(164\;cm\). Chiều dài mỗi con lắc lần lượt là
Một con lắc đơn có độ dài \(l\) được thả không vận tốc ban đầu từ vị trí biên có biên độ góc \({\alpha _0}\) \(\left( {\alpha \le {{10}^0}} \right)\). Bỏ qua mọi ma sát. Khi con lắc đi qua vị trí có li độ góc \(\alpha \) thì tốc độ của con lắc là
Con lắc lò xo gồm vật \(m = 100\;g\) và lò xo có độ cứng \(k = 100\;N/m\), ( cho \({\pi ^2} = 10\) ) dao động điều hòa với chu kì
Một con lắc lò xo gồm một lò xo khối lượng không đáng kể, độ cứng k, một đầu cố định và một đầu gắn với một viên bi nhỏ khối lượng m. Chu kỳ biến thiên tuần hoàn của động năng con lắc là
Cho một sóng ngang có phương trình sóng là \(u = 8\sin 2\pi \left( {\frac{t}{{0,1}} - \frac{x}{{50}}} \right)mm\), trong đó \(x\) tính bằng \(cm\), \(t\) tính bằng giây. Bước sóng là
Dao động tại hai điểm \({S_1},{S_2}\) cách nhau \(10\;cm\) trên mặt chất lỏng có cùng biểu thức \(u = \) \({\mathop{\rm acos}\nolimits} 40\pi t\). Tốc độ truyền sóng trên mặt chất lỏng là \(40\;cm/s\). Trong khoảng \({S_1}\;{S_2}\), số điểm dao động với biên độ cực đại là
Một con lắc đơn dao động điều hòa tại nơi có \(g = {\pi ^2}\;m/{s^2}\) thì người ta đo được chu kì của nó là \(T = 1\) giây. Chiều dài của con lắc là
Sóng cơ có tần số \(80\;Hz\) lan truyền trong một môi trường với vận tốc \(4\;m/s\). Dao động của các phần tử vật chất tại hai điểm trên một phương truyền sóng cách nguồn sóng những đoạn lần lượt \(31\;cm\) và \(33,5\;cm\), lệch pha nhau góc
