Các mức năng lượng của các trạng thái dừng của nguyên tử hiđro được xác định bằng biểu thức \({E_n} = - \frac{{13,6}}{{{n^2}}}\left( {{\rm{eV}}} \right)\left( {{\rm{n}} = 1,2,3, \ldots } \right)\). Cho các hằng số \({\rm{h}} = 6,{625.10^{ - 34}}{\rm{Js}};{\rm{c}} = {3.10^8}{\rm{\;m}}/{\rm{s}};{\rm{e}} = \) 1,6.10-19 C. Nếu nguyên tử hiđro hấp thụ một photon có năng lượng 2,856 eV thì bước sóng nhỏ nhất của bức xạ mà nguyên tử hiđro đó có thể phát ra là
D. \(9,{514.10^{ - 8}}{\rm{\;m}}\)
 Giải bởi Vietjack
Giải bởi Vietjack
\(\Delta E = {E_C} - {E_T} = - \frac{{13,6}}{{{n_C}^2}} + \frac{{13,6}}{{{n_T}^2}} = 2,856 \Rightarrow {n_C} = \sqrt {\frac{{13,6}}{{\frac{{13,6}}{{{n_T}^2}} - 2,856}}} \to \)TABLE \( \Rightarrow \left\{ \begin{array}{l}{n_T} = 2\\{n_C} = 5\end{array} \right.\)
Bước sóng nhỏ nhất phát ra khi từ quỹ đạo 5 về 1
\[\frac{{hc}}{\lambda } = {E_5} - {E_1} \Rightarrow \lambda = \frac{{hc}}{{{E_5} - {E_1}}} = \frac{{1,{{9875.10}^{ - 25}}}}{{\left( { - \frac{{13,6}}{{{5^2}}} + \frac{{13,6}}{{{1^2}}}} \right).1,{{6.10}^{ - 19}}}} \approx 9,{514.10^{ - 8}}m\]. Chọn D
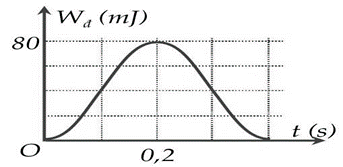
Một vật khối lượng \(400{\rm{\;g}}\) đang thực hiện dao động điều hòa. Đồ thị bên mô tả động năng của vật theo thời gian t. Lấy \({\pi ^2} = 10\). Biên độ dao động của vật là
Sắp xếp theo thứ tự tăng dần bước sóng với các ánh sáng đỏ, vàng, lam là
Một máy biến áp lí tưởng có số vòng dây của cuộn sơ cấp là 500 vòng và thứ cấp là 200 vòng. Đặt vào hai đầu cuộn sơ cấp điện áp xoay chiều có giá trị hiệu dụng \(100{\rm{\;V}}\) thì điện áp hiệu dụng ở hai đầu cuộn thứ cấp để hở là
Hai nguồn phát sóng kết hợp A, B trên mặt nước cách nhau \(10{\rm{\;cm}}\) dao động theo phương trình \({u_1} = {u_2} = 2{\rm{cos}}40\pi t\;\left( {{\rm{cm}}} \right)\). Xét điểm \({\rm{M}}\) trên mặt nước cách \({\rm{A}},{\rm{B}}\) sao cho \({\rm{MA}} = 4,2{\rm{\;cm}}\) và \({\rm{MB}} = 9{\rm{\;cm}}\). Coi biên độ sóng không đổi và tốc độ truyền sóng trên mặt nước là \({\rm{v}} = 32{\rm{\;cm}}/{\rm{s}}\). Giữ nguyên tần số \(f\) và các vị trí \(A,M\). Cân dịch chuyển nguồn \(B\) xa nguồn \(A\) (dọc theo phương \(AB)\) một đoạn nhỏ nhất bao nhiêu để tại \(M\) là một cực tiểu giao thoa?
Đặt một điện áp xoay chiều có giá trị hiệu dụng không đổi, tần số \(f\) thay đổi được vào hai đầu đoạn mạch \({\rm{MN}}\) gồm cuộn dây mắc nối tiếp với ampe kế \({\rm{A}}\) (ampe kế nhiệt lí tưởng) như hình bên. Khi tăng tần số \(f\) thì chỉ số của ampe kế thay đổi như thế nào?
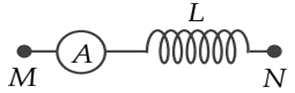
Đặt điện áp xoay chiều \(u = U\sqrt 2 {\rm{cos}}\left( {\omega t + {\varphi _u}} \right)\) vào hai đầu tụ điện có điện dung C, thì dòng điện qua mạch có biểu thức \(i = I\sqrt 2 {\rm{cos}}\left( {\omega t + {\varphi _i}} \right)\). Biểu thức nào sau đây đúng?
Trong mạch dao động LC lí tưởng đang có dao động điện từ tự do. Gọi q là điện tích của một bản tụ điện và i là cường độ dòng điện trong mạch. Phát biểu nào sau đây đúng?
Hai dao động điều hòa với cùng phương, cùng tần số có biên độ và pha ban đầu lần lượt là \({A_1},{\varphi _1}\) và \({A_2},{\varphi _2}\). Dao động tổng hợp của hai dao động trên có biên độ là \(A\). Khi hiệu \({\varphi _1} - {\varphi _2}\) \( = \left( {2n + 1} \right)\pi \) với \(n = 0, \pm 1, \pm 2, \ldots \) thì giá trị của \({\rm{A}}\) là
Trong hiện tượng huỳnh quang, nếu ánh sáng kích thích là ánh sáng màu lam thì ánh sáng huỳnh quang không thể là ánh sáng nào sau đây?
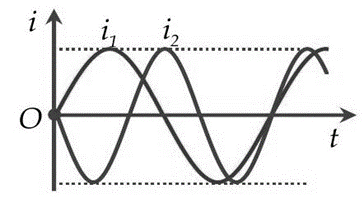
Hai mạch dao động điện từ lí tưởng đang có dao động điện từ tự do với các cường độ dòng điện i1 và i2 được biểu diễn trên cùng đồ thị như hình vẽ. Khi \({{\rm{i}}_1} = {{\rm{i}}_2} < {{\rm{I}}_0}\) thì tỉ số độ lớn điện tích \({{\rm{q}}_1}/{{\rm{q}}_2}\) có thể có giá trị nào sau đây?
Một điện tích điểm có độ lớn điện tích là \(Q\) đặt trong chân không. Độ lớn cường độ điện trường ở điểm cách điện tích khoảng \(r\) là