Cho hình vẽ
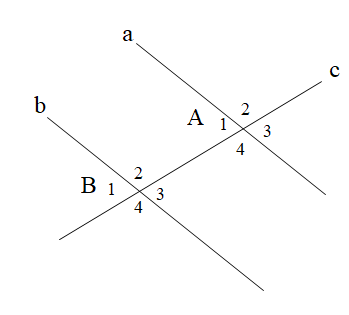
Biết một cặp góc đồng vị \[\widehat {{A_4}} = \widehat {{B_4}} = 60^\circ \]. Tính số đo của cặp góc đồng vị \[\widehat {{A_3}}\] và \[\widehat {{B_3}}\].
A. 120°;
B. 50°;
C. 60°;
D. 150°.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A

Ta có:
\[\widehat {{A_4}} + \widehat {{B_3}} = 180^\circ \] (hai góc kề bù)
Do đó \[\widehat {{B_3}} = 180^\circ - 60^\circ = 120^\circ \]
Suy ra \[\widehat {{A_3}}\; = \widehat {{B_3}} = 120^\circ \]
Vậy chọn đáp án A.
Biết một cặp góc so le trong \[\widehat {{A_4}}\; = \widehat {{B_2}} = 110^\circ \]. Tính số đo của cặp góc so le trong còn lại:

Cho hình vẽ
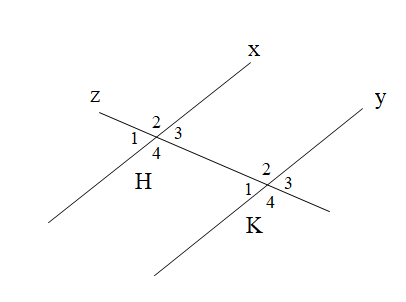
Biết x // y, \[\widehat {{H_3}} = 39^\circ .\]Tính \[\widehat {{H_3}} + \widehat {{K_4}}\].
Cho hình vẽ dưới đây:
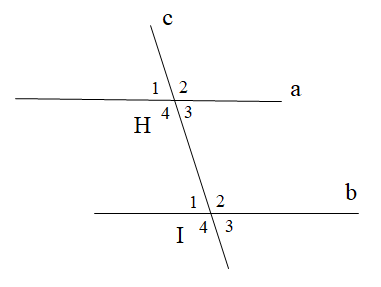
\[\widehat {{H_1}}\] và \[\widehat {{I_1}}\] là hai góc:
A. Kề bù;
Cho hình vẽ
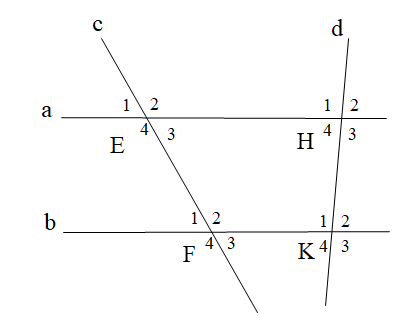
Biết a // b,
\[{\widehat E_1} = 48^\circ \]. Số đo \[\widehat {{F_3}}\] là:
Cho tia Ot nằm trong góc mOn, \[\widehat {mOt} = \widehat {tOn}\] thì
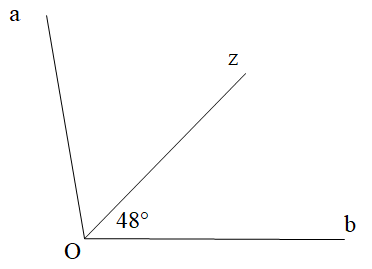
Tính số đo của góc aOb. Biết \[\widehat {zOb} = 48^\circ \], Oz là tia phân giác của góc aOb.
Cho hình vẽ

Biết x // y, \[\widehat {{H_3}} = 39^\circ \]. Tính số đo \[\widehat {{K_3}}\]
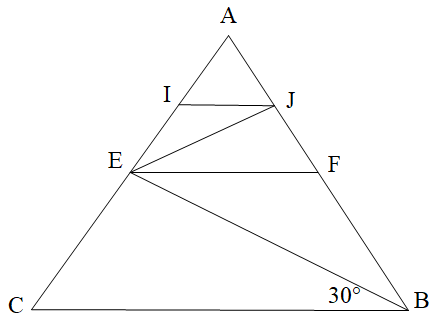
Cho hình vẽ bên dưới. Tính \(\widehat {BEF}\), biết FE // BC và \(\widehat {EBC} = 30^\circ \).
Chọn đáp án đúng.
Nếu đường thẳng c cắt hai đường thẳng a, b và a // b thì:
(I) Hai góc đồng vị bằng nhau
(II) Hai góc so le trong bằng nhau
(III) Hai góc bù nhau bằng nhau
(IV) Hai góc kề bù bằng nhau
Cho \(\widehat {xOy} = 66^\circ \), tia Ot là tia phân giác của góc xOy. Số đo góc xOt là:
Cho \[\widehat {MON} = 90^\circ \] và vẽ tia OP sao cho tia ON là tia phân giác của góc MOP. Khi đó góc MOP là: