Cho ΔABC cân tại A, AB = AC = 5 cm; BC = 8 cm. Kẻ AH\[ \bot \]BC (H\( \in \)BC).
a) Chứng minh HB = HC.
b) Tính AH.
c) Kẻ HD\[ \bot \]AB (D\( \in \)AB); HE\[ \bot \]AC (E\( \in \)AC). Chứng minh: ΔHDE là tam giác cân.
 Giải bởi Vietjack
Giải bởi Vietjack
|
GT |
ΔABC cân tại A, AB = AC = 5 cm; BC = 8 cm. AH\[ \bot \]BC (H\( \in \)BC); HD\[ \bot \]AB (D\( \in \)AB); HE\[ \bot \]AC (E\( \in \)AC). |
|
KL |
a) Chứng minh HB = HC. b) Tính AH. c) ΔHDE là tam giác cân. |
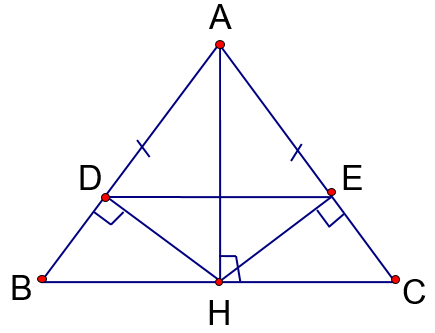
a) Xét ∆ABH và ∆ACH có:
\(\widehat {AHB} = \widehat {AHC} = {90^o}\)
AB = AC = 5 cm
Cạnh AH chung
Do đó ∆ABH = ∆ACH (cạnh huyền – cạnh góc vuông)
Suy ra BH = CH (hai cạnh tương ứng)
b) Từ câu a: BH = CH suy ra \(BH = \frac{{BC}}{2} = \frac{8}{2} = 4\,\,(cm)\).
Áp dụng định lý Py-ta-go vào ∆AHB vuông tại H, ta có:
AB2 = AH2 + BH2
\( \Rightarrow \) AH2 = AB2 − BH2 = 52 − 42 = 25 – 16 = 9.
Do đó \(AH = \sqrt 9 = 3\,\,(cm)\)
c) Xét ∆DBH và ∆ECH có:
\(\widehat B = \widehat C\) (vì ∆ABC cân tại A)
BH = CH (cmt)
\(\widehat {BDH} = \widehat {HEC} = {90^o}\)
Do đó ∆ABH = ∆ACH (cạnh huyền – góc nhọn)
Suy ra DH = EH (hai cạnh tương ứng).
Vậy ∆DHE cân tại H.
Cho đơn thức: A = (2x2y3).(−3x3y4)
a) Thu gọn đơn thức A.
b) Xác định hệ số và bậc của đơn thức A sau khi đã thu gọn.
Điểm kiểm tra cuối học kì I môn vật lý của lớp 7A được bạn lớp trưởng ghi lại như sau:
|
5 |
8 |
4 |
8 |
6 |
6 |
5 |
7 |
4 |
3 |
6 |
7 |
|
7 |
3 |
8 |
6 |
7 |
6 |
5 |
9 |
7 |
9 |
7 |
4 |
|
4 |
7 |
10 |
6 |
7 |
5 |
4 |
7 |
6 |
5 |
2 |
8 |
a) Dấu hiệu ở đây là gì? Số các giá trị là bao nhiêu?
b) Lập bảng “tần số” và tìm mốt của dấu hiệu.
c) Tính số trung bình cộng của dấu hiệu.
Trên tia phân giác góc A của tam giác ABC (AB > AC) lấy điểm M. Chứng minh |MB – MC| < AB – AC.