Cho hình dưới đây:
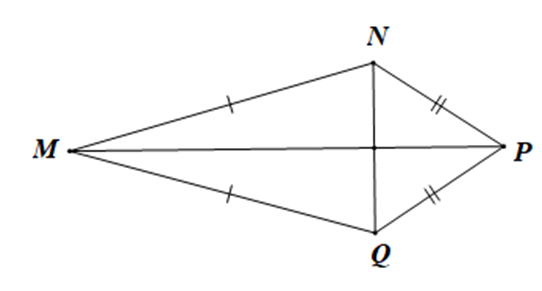
Xét các khẳng định:
(1) MP là tia phân giác của \(\widehat {NMQ}\);
(2) NQ là tia phân giác của \(\widehat {MNP}\).
Chọn khẳng định đúng:
A. Chỉ có (1) đúng;
B. Chỉ có (2) đúng;
C. Cả (1) và (2) đều đúng;
D. Cả (1) và (2) đều sai.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
+ Xét tam giác MNP và tam giác MPQ có:
MN = MQ, NP = QP, MP là cạnh chung
Suy ra DMNP = DMQP (c.c.c)
Do đó \(\widehat {NMP} = \widehat {QMP}\) (hai góc tương ứng)
Nên MP là tia phân giác của \(\widehat {NMQ}\). Do đó (1) là đúng.
+ Xét khẳng định (2): NQ là tia phân giác của \(\widehat {MNP}\).
Để NQ là tia phân giác của \(\widehat {MNP}\) thì \(\widehat {MNQ} = \widehat {QNP}\) nhưng không có dữ kiện nào để khẳng định điều này.
Vậy chỉ có (1) đúng.
Cho hai tam giác ABC và OHK có AB = OH, AC = HK. Điều kiện để DABC = DHOK theo trường hợp cạnh – cạnh – cạnh là:
Xét bài toán “DOAB và DOAC có AB = AC, OB = OC (điểm O nằm ngoài tam giác ABC). Chứng minh rằng \(\widehat {OAB} = \widehat {OAC}\).”
Cho các câu sau:
(1) Suy ra DOAB = DOAC (c.c.c);
(2) AB = AC (giả thiết),
OB = OC (giả thiết),
OA là cạnh chung;
(3) Do đó \(\widehat {OAB} = \widehat {OAC}\) (hai góc tương ứng).
(4) Xét DOAB và DOAC có:
Hãy sắp xếp một cách hợp lí các câu trên để giải bài toán.
Trên hình vẽ dưới đây:
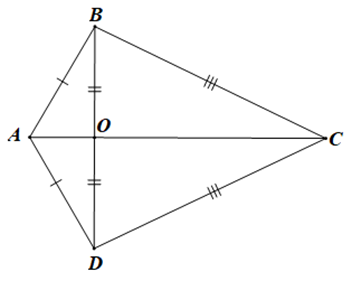
Số cặp tam giác bằng nhau theo trường hợp cạnh – cạnh – cạnh là:
Cho hình vẽ bên dưới:
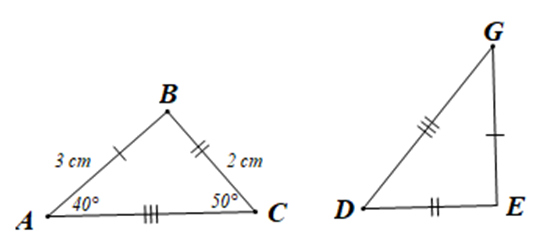
Số đo góc DGE và độ dài cạnh EG lần lượt là:
Cho hình vẽ dưới đây:
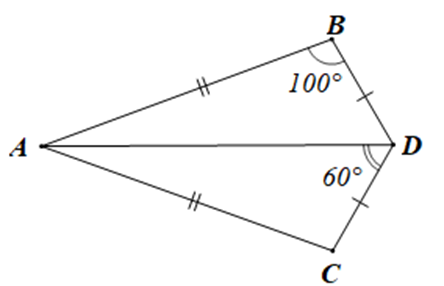
Số đo của \(\widehat {BAC}\) trong hình vẽ trên bằng:
Cho tam giác ABC có AB = AC, M là trung điểm của BC. Biết \(\widehat {ABC} = 40^\circ ,\) số đo của \(\widehat {BAM}\) là:
Cho tam giác ABC, vẽ cung tròn tâm A bán kính BC, vẽ cung tròn tâm B bán kính AC, hai dây cung này cắt nhau tại D (D và C nằm khác phía so với đường thẳng AB). Khẳng định nào sau đây là đúng?
Cho tam giác ABC (AB < AC). Trên cạnh AC lấy điểm D sao cho AB = AD. Lấy M là trung điểm của BC. Qua C kẻ đường thẳng vuông góc với BD tại N. Chọn khẳng định sai: