Cho đường thẳng xy và một điểm A không thuộc đường thẳng xy. Lấy hai điểm B và C sao cho AB // xy, AC // xy. Khi đó khẳng định nào sau đây đúng?
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: A
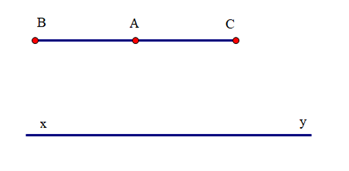
+ Theo tiên đề Euclid: chỉ có một đường thẳng đi qua A và song song với xy
Mà hai đường thẳng AB và AC đều đi qua A và song song với xy
Suy ra hai đường thẳng AB và AC trùng nhau.
Do đó ba điểm A, B, C thẳng hàng.
Suy ra các khẳng định A là đúng, B và D là sai.
Ta xét trường hợp B nằm giữa A và C (hình vẽ)
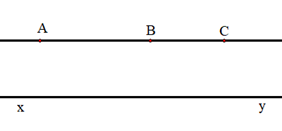
Vì B nằm giữa A và C (theo điều giả sử)
Suy ra AC = AB + BC.
Do đó khẳng định C là sai.
Vậy ta chọn phương án A.
Cho đường thẳng c cắt hai đường thẳng song song a và b. Khi đó tiên đề Euclid suy ra tính chất nào sau đây:
Cho tam giác ABC. Qua đỉnh A vẽ đường thẳng a song song với BC, qua đỉnh B vẽ đường thẳng b song song với AC. Số đường thẳng a, b vẽ được lần lượt là:
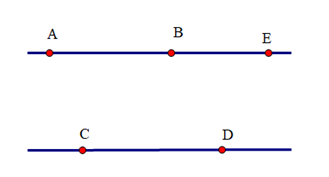
Cho AB // CD. Trên tia đối của tia BA lấy điểm E. Chứng minh BE // CD.
Cho tam giác ABC. Lấy hai điểm phân biệt M, N sao cho AM // BC; AN // BC như hình vẽ:
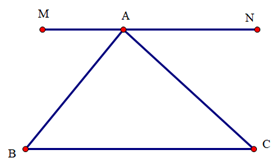
Khi đó:
Cho hình vẽ và các khẳng định sau:
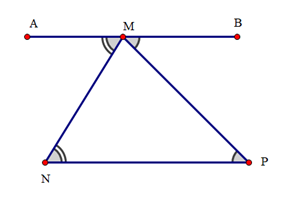
(I). AM // NP;
(II). MB // NP;
(III). A, M, B thẳng hàng.
Có bao nhiêu khẳng định đúng trong các khẳng định trên?