Chọn phát biểu sai:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
Hai góc đối đỉnh là hai góc bằng nhau nên A đúng.
Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia nên B đúng.

Hai đường thẳng xy và zt cắt nhau tại O (như hình vẽ trên). Ta có \({\widehat {\rm{O}}_1}\) và \({\widehat {\rm{O}}_2}\); \({\widehat {\rm{O}}_3}\) và \({\widehat {\rm{O}}_4}\) là hai cặp góc đối đỉnh. Do đó hai đường thẳng cắt nhau tại một điểm tạo thành hai cặp góc đối đỉnh nên C đúng.
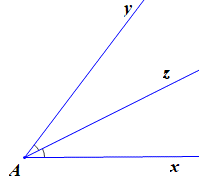
Quan sát hình vẽ trên có: \(\widehat {x{\rm{A}}z} = \widehat {{\rm{yAz}}}\) mà hai góc này ở vị trí kề nhau.
Do đó hai góc bằng nhau chưa chắc là hai góc ở vị trí đối đỉnh nên D sai.
Vậy ta chọn phương án D.
Quan sát hình vẽ.
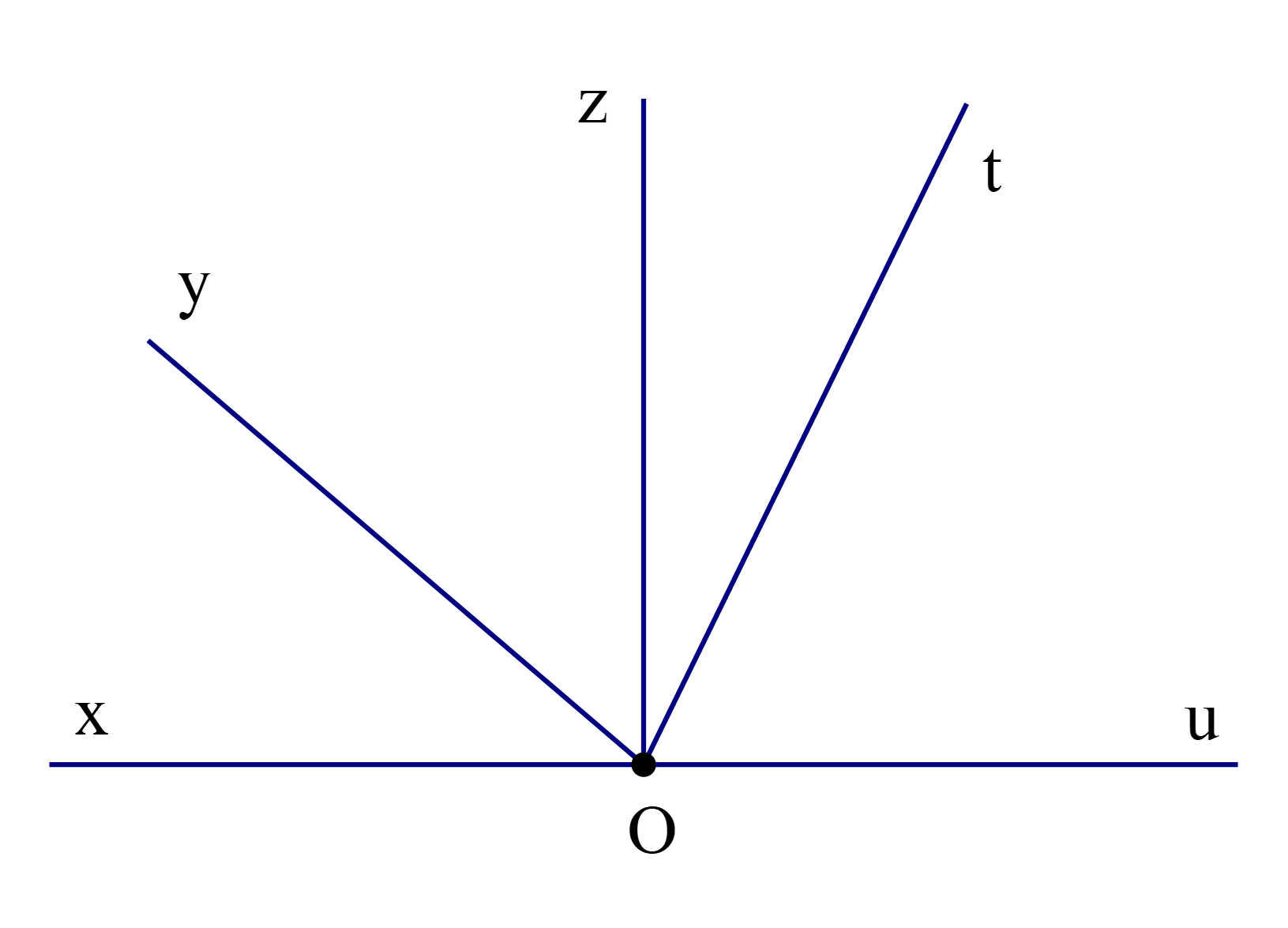
Có tất cả bao nhiêu góc kề (không kể góc bẹt) với \(\widehat {{\rm{xOy}}}\)?