Cho hình vẽ, biết rằng \(\widehat {{\rm{AMC}}} - \widehat {{\rm{AMB}}} = 80^\circ \).
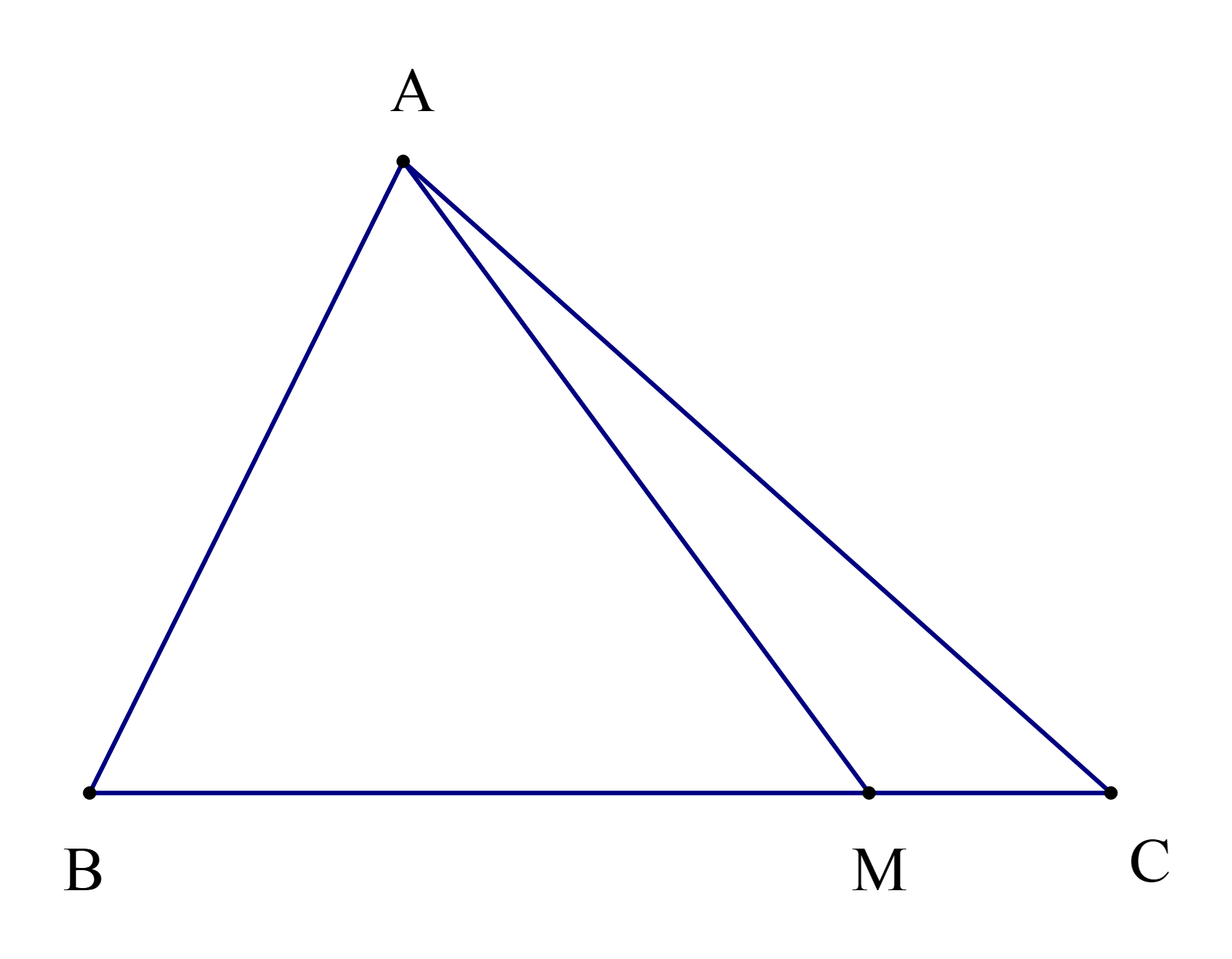
Chọn khẳng định đúng:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
Theo bài ta có: \(\widehat {{\rm{AMC}}} - \widehat {{\rm{AMB}}} = 80^\circ \)
Suy ra \(\widehat {{\rm{AMC}}} = 80^\circ + \widehat {{\rm{AMB}}}\) (1)
Ta lại có \(\widehat {{\rm{AMB}}}\) và \(\)\(\widehat {{\rm{AMC}}}\) là hai góc kề bù nên:
\(\widehat {{\rm{AMB}}}{\rm{ + }}\widehat {{\rm{AMC}}} = 180^\circ \) (2)
Thay (1) vào (2) ta có:
\(\widehat {{\rm{AMB}}}{\rm{ + 80}}^\circ {\rm{ + }}\widehat {{\rm{AMB}}} = 180^\circ \)
Suy ra \(2\widehat {{\rm{AMB}}} = 180^\circ - 80^\circ = 100^\circ \)
Suy ra \(\widehat {{\rm{AMB}}} = \frac{{100^\circ }}{2} = 50^\circ \)
Thay \(\widehat {{\rm{AMB}}} = 50^\circ \) vào (1) ta có:
\(\widehat {{\rm{AMC}}} = 80^\circ + 50^\circ = 130^\circ \)
Vậy \(\widehat {{\rm{AMB}}} = 50^\circ \);\(\widehat {{\rm{AMC}}} = 130^\circ \).
Cho hình vẽ.
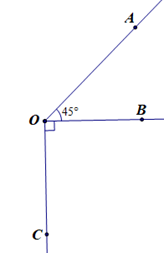
Kẻ tia OE là tia đối của tia OB và tia OD nằm giữa hai tia OC và OE sao cho \(\widehat {{\rm{COD}}} = \widehat {{\rm{DOE}}}.\) Chọn khẳng định sai:
Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo AC và BD sao cho \(\widehat {{\rm{AOB}}} = 2\widehat {{\rm{AOD}}} = 4\widehat {{\rm{ODC}}}\). Chọn khẳng định đúng: