Cho hình dưới đây:
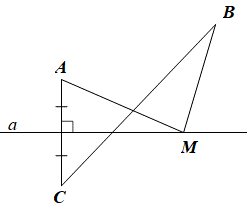
Biết điểm M là điểm bất kì nằm trên đường thẳng a. Khẳng định đúng là:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
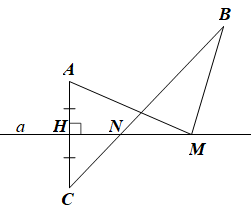
Đường thẳng a ⊥ AC tại trung điểm H của AC nên a là đường trung trực của AC.
Vì M nằm trên đường trung trực a của AC nên MA = MC.
+) Nếu M ≠ N thì MA + MB = MC + MB.
Xét DMBC có MB + MC > BC (bất đẳng thức trong tam giác)
Do đó MA + MB > BC (1)
+) Nếu M ≡ N:
Gọi N là giao điểm của a và BC.
Vì N nằm trên đường trung trực của AC nên NA = NC.
Khi đó MA + MB = NA + NB = NC + NB = BC (2)
Từ (1) và (2) suy ra MA + MB ≥ BC.
Vậy ta chọn phương án D.
Cho ∆MNP cân tại M có \[\widehat {\rm{N}} = 50^\circ \] và MO là đường trung trực của NP (O ∈ NP). Số đo của \(\widehat {{\rm{OMP}}}\) là
Cho đoạn thẳng AB = 5 cm. Vẽ đường tròn tâm A, bán kính 4 cm và đường tròn tâm B, bán kính 3 cm. Hai đường tròn này cắt nhau tại D và E. Khẳng định nào sau đây đúng nhất?
Cho \(\widehat {{\rm{xOy}}} = 30^\circ \). Trên tia Ox lấy điểm E, trên tia Oy lấy điểm F. Lấy điểm D sao cho OF là đường trung trực của ED. Chọn khẳng định đúng:
Cho ∆ABC cân tại A có \(\widehat {{\rm{BAC}}} = 82^\circ \), đường trung trực của AB cắt BC tại D. Số đo của \(\widehat {{\rm{ADB}}}\) là
Cho hình vẽ, biết AC = 8 cm và chu vi ∆ABC bằng 22 cm.

Độ dài cạnh BC là