Cho ∆ABC, gọi I là giao điểm của hai đường trung trực của hai cạnh AB và AC. Kết quả nào dưới đây đúng?
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
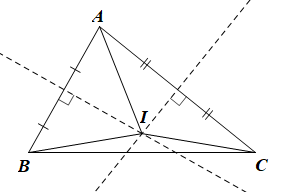
∆ABC có I là giao điểm của hai đường trung trực của hai cạnh AB và AC.
Suy ra I cũng thuộc đường trung trực của cạnh BC.
Vì giao điểm I của ba đường trung trực cách đều ba đỉnh của ∆ABC.
Nên IA = IB = IC.
Vậy ta chọn phương án B.
Cho các nhận xét sau:
(I) Giao điểm của ba đường trung trực trong một tam giác bất kì luôn nằm trong tam giác đó;
(II) Giao điểm của ba đường trung trực trong tam giác vuông nằm trên cạnh huyền của tam giác vuông đó;
(III) Giao điểm của ba đường trung trực trong tam giác nhọn nằm ngoài tam giác đó;
(IV) Giao điểm của ba đường trung trực trong tam giác tù nằm ngoài tam giác đó.
Có bao nhiêu nhận xét đúng?
Cho các hình vẽ sau:
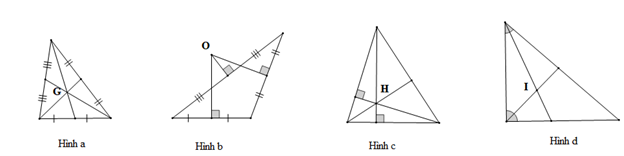
Hình nào có giao điểm của ba đường trung trực ?