Cho tam giác XYZ nhọn, đường cao XA. Lấy B thuộc đoạn AZ, vẽ BC vuông góc XZ. Giao điểm của XA và BC là I. Khẳng định nào sau đây là đúng?
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
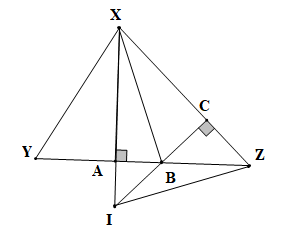
Vì DXYZ nhọn nên \(\widehat {{\rm{YX}}Z} < 90^\circ \), do đó B là khẳng định sai.
Vì CB ⊥ XZ, \(\widehat {{\rm{YX}}Z} < 90^\circ \)nên XY và IC không song song với nhau.
Do đó A là khẳng định sai.
Xét DIXZ có IC, ZA là hai đường cao cắt nhau tại B nên B là trực tâm tam giác XIZ.
Do đó XB ⊥ IZ, nên C là khẳng định đúng.
Vậy ta chọn phương án C.
Cho tam giác MNP có \(\widehat M = 63^\circ ,\widehat N = 48^\circ \). Vẽ trực tâm O của tam giác MNP. Số đo góc MON là:
Cho tam giác ABC có \(\widehat B = 50^\circ ,\widehat C = 30^\circ \). Vẽ đường cao AH, phân giác AE. Trên cạnh AC lấy D sao cho \(\widehat {CB{\rm{D}}} = 10^\circ \). Gọi I là giao điểm của AE và BD. Số đo góc AID là:
Cho tam giác ABC vuông tại A, trên tia BA lấy M sao cho BM = BC. Tia phân giác góc B cắt AC tại H. Khẳng định nào sau đây là sai?
Cho tam giác IHK đều có G là trọng tâm. Khẳng định nào sau đây là đúng?
Cho tam giác ABC nhọn có đường cao AI. Trên AI lấy E sao cho \(\widehat {BAI} = \widehat {BCE}.\) Gọi F là giao điểm của AB và CE, H là giao điểm của BE và AC. Khẳng định nào sau đây là sai?