Cho ∆ABC và ∆DEF có AB = DF, AC = DE và BC = FE. Khẳng định nào sau đây đúng?
A. ∆ABC = ∆DFE;
B. ∆ABC = ∆DEF;
C. ∆ABC = ∆EFD;
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
Xét ∆ABC và ∆DFE, có:
AB = DF (giả thiết)
AC = DE (giả thiết)
BC = FE (giả thiết)
Do đó ∆ABC = ∆DFE (c.c.c)
Vậy ta chọn phương án A.
Quan sát hình bên.
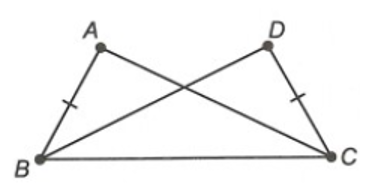
Để ∆ABC = ∆DCB theo trường hợp cạnh – cạnh – cạnh thì cần thêm điều kiện:
Cho ∆ABC có AB = AC. Gọi D, E là hai điểm thuộc cạnh BC sao cho BD = DE = EC. Biết AD = AE. Khẳng định nào sau đây đúng nhất?
Cho ∆ABC và ∆MNP bằng nhau. Biết số đo các góc như hình vẽ sau:
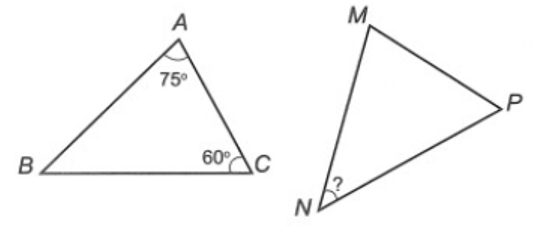
Số đo của bằng:
Cho ∆ABC có M là trung điểm BC, N là một điểm nằm bên trong ∆ABC sao cho NB = NC. Kết luận nào sau đây đúng?