Cho hình vẽ bên.
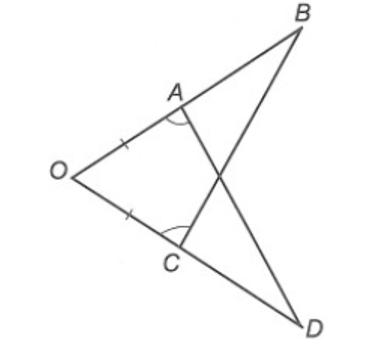
Cặp tam giác nào sau đây bằng nhau?
A. ∆OAC và ∆OBD;
B. ∆OAD và ∆OCB;
C. ∆ABC và ∆BCD;
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
⦁ Xét ∆OAD và ∆OCB, có:
(giả thiết)
OA = OC (giả thiết)
là góc chung.
Do đó ∆OAD = ∆OCB (g.c.g)
Vì vậy phương án B đúng.
⦁ Phương án A sai vì OA < OB và A ∈ OB.
⦁ Phương án C, D sai vì không có các cặp cạnh, cặp góc tương ứng thỏa mãn cả ba trường hợp bằng nhau của hai tam giác.
Vậy ta chọn phương án B.
Cho ∆ABC và ∆MNP có AB = NM, AC = NP và . Trong các khẳng định sau, khẳng định nào sai?
Điền từ còn thiếu vào chỗ chấm để được phát biểu đúng:
Nếu hai ... và góc xen giữa của tam giác này bằng hai cạnh và ... xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
Cho ∆ABC = ∆MNP (c – g – c). Đỉnh A và B của tam giác ABC tương ứng với đỉnh nào của tam giác MNP?