Cho tam giác QJN cân tại Q có QR là tia phân giác góc JQN (R ∈ JN). Trên QR lấy điểm S. Tam giác SJN là tam giác
A. Tam giác vuông;
B. Tam giác cân;
C. Tam giác đều;
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
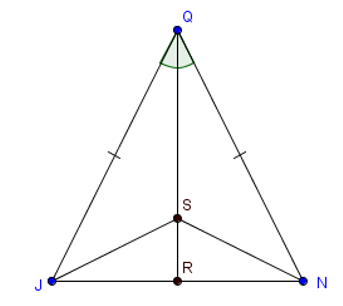
Tam giác JQN cân tại Q nên QJ = QN (tính chất)
Xét ∆JQR và ∆NQR có
QJ = QN
(QR là phân giác góc JQN)
QR là cạnh chung
Suy ra ∆JQR = ∆NQR (c.g.c)
Do đó JR = NR (hai cạnh tương ứng) suy ra R là trung điểm của JN (1)
(hai góc tương ứng)
Mà (kề bù)
Suy ra
Do đó QR ⊥ JN tại R (2)
Từ (1) và (2) suy ra QR là đường trung trực của JN.
S ∈ QR (giả thiết) suy ra SJ = SN (tính chất đường trung trực)
Do đó tam giác SJN cân tại S.
Cho ∆ABC vuông tại A có AB < AC, kẻ đường phân giác BD của góc ABC, (D ∈ AC). Kẻ DM vuông góc với BC tại M. Khẳng định nào dưới đây sai?
Cho điểm M thuộc đường trung trực của đoạn thẳng AB sao cho góc MAB bằng 60°. Khẳng định đúng là
Cho tam giác MNP có MP = 9 cm, NP = 16 cm. Vẽ đường trung trực của MN cắt NP tại K. Chu vi tam giác KMP là
Cho ba điểm phân biệt H, I, K thẳng hàng, điểm I nằm giữa H và K. Gọi m và n lần lượt là đường trung trực của HI và IK. Khẳng định đúng là
Cho tam giác ABC đều cạnh 20 cm. Trên AB lấy D sao cho AD = 8 cm. Đường trung trực của AD cắt AC tại D. Chu vi tứ giác BCFD là
Cho đường thẳng d là đường trung trực của đoạn thẳng HI (d cắt HI tại O). Điểm M không thuộc đường thẳng d và đoạn thẳng HI sao cho đường thẳng d cắt đoạn thẳng MI tại P. Khẳng định nào dưới đây đúng?