Một con lắc lò xo treo thẳng đứng, dao động điều hòa tại nơi có \(g = 10m/{s^2}\). Hình bên là đồ thị biểu diễn sự phụ thuộc của độ lớn lực kéo về \({F_{kv}}\) tác dụng lên vật và độ lớn lực đàn hồi của lò xo theo thời gian. Biết \({t_2} - {t_1} = \frac{{7\pi }}{{120}}\) (s). Khi lò xo dãn 6,5 cm thì tốc độ của vật
D. 80 cm/s
Giải bởi Vietjack
Đáp án : B.
Đựa vào đồ thị ta có \[\frac{{{F_{{\rm{d}}hmax}}}}{{{F_{kvmax}}}} = \frac{{k(\Delta {l_0} + A)}}{{k.A}} = \frac{{\Delta {l_0} + A}}{A} = \frac{3}{2} \to A = 2\Delta {l_0}\](1)
Tại thời điểm t =t1 thì Fđh = 0, vật ở vị trí lò xo không biến dạng. Lúc này x1 = -Δl0(2)
Tại thời điểm t2 thì Fkv = 0, chứng tỏ vật ở VTCB lần thứ 2 kể từ t1. Do đó ta có thời gian đi từ t1 đến t2 là t2 – t1 = \[{t_{ - \Delta {l_0} \to 0( - \frac{A}{2} \to 0)}} + {t_{0 \to A}} + {t_{A \to 0}} = \frac{T}{{12}} + \frac{T}{4} + \frac{T}{4} = \frac{{7T}}{{12}} = \frac{{7\pi }}{{120}} \to T = \frac{\pi }{{10}} \to \omega = 20\](rad/s).
Mặt khác ta có \[\omega = \sqrt {\frac{g}{{\Delta {l_0}}}} \to \Delta {l_0} = \frac{g}{{{\omega ^2}}} = \frac{{10}}{{{{20}^2}}} = 0,025\](m) = 2,5 cm. (3). Thay (3) vào (1) ta có A = 5 cm.
Khi lò xo dãn 6,5 cm. suy ra li độ lúc đó là: x = 6,5 -2,5 = 4 cm.
Vậy tốc độ của vật là v =\[\omega \sqrt {{A^2} - {x^2}} = 20\sqrt {{5^2} - {4^2}} = 60\](cm/s)
Một chất điểm dao động điều hòa với phương trình \(x = A\cos (\omega t + \varphi )\), biểu thức vận tốc tức thời của chất điểm là
Một vật dao động điều hòa với tần số góc \(\omega \). Thế năng của vật ấy
Một sợi dây hai đầu cố định sóng phản xạ so với sóng tới tại điểm cố định sẽ không cùng
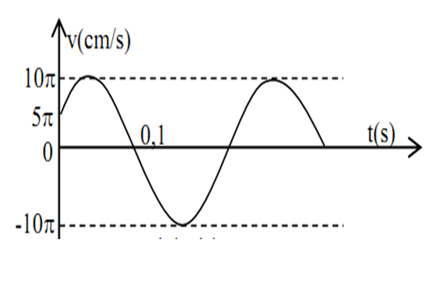
Một vật dao động điều hoà có độ thị vận tốc – thời gian như hình vẽ. Phương trình dao động của vật
Một chất điểm dao động điều hòa trên trục Ox. Khi chất điểm đi qua vị trí cân bằng thì tốc độ của nó là \({\rm{20}}\;cm/s\). Khi chất điểm có tốc độ là \({\rm{10}}\;cm/s\) thì gia tốc của nó có độ lớn là \({\rm{40}}\sqrt 3 \;cm/{s^2}\). Biên độ dao động của chất điểm là
Một con lắc đơn dao động theo phương trình \(s = 4\cos 2\pi t(\;cm)\) (\(t\) tính bằng giây). Chu kì dao động của con lắc là
Sóng cơ lan truyền trong môi trường với tốc độ v không đổi, khi tăng tần số sóng lên 5 lần thì bước sóng sẽ
Một vật dao động điều hòa với tần số góc \({\rm{5}}rad/s\). Khi vật đi qua li độ \({\rm{5}}\;cm\) thì nó có tốc độ là \({\rm{25}}\)cm/s. Biên độ dao động của vật là
Con lắc lò xo treo thằng đứng đang dao động điều hòa tại nơi có gia tốc trọng trường g. Khi cân bằng, lò xo dãn một đoạn \(\Delta {l_0}\). Chu kì dao động của con lắc có thể xác định theo biểu thức nào sau đây:
Một vật khối lượng \(m\), dao động điều hòa với phương trình \(x = A\cos (\omega t)\). Mốc thế năng ở vị trí cân bằng, động năng cực đại của vật này bằng
Trên mặt nước có hai nguồn sóng nước giống nhau cách nhau \(AB = 8(\;cm)\). Sóng truyền trên mặt nước có bước sóng \(1,2(\;cm)\). Số đường cực đại đi qua đoạn thẳng nối hai nguồn là
Một con lắc lò xo gồm vật nhỏ và lò xo nhẹ có độ cứng k, dao động điều hoà dọc theo trục \(Ox\) quanh vị trí cân bằng \(O\). Biểu thức lực kéo về tác dụng lên vật theo li độ \(x\) là:
Một vật nhỏ dao động điều hòa thực hiện \({\rm{2020}}\) dao động toàn phần trong \({\rm{505}}\;s\). Tần số dao động của vật là
