Cho ∆ABC có G là trọng tâm như hình vẽ.
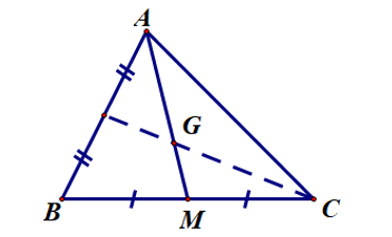
Biết AG = 4x + 6 và AM = 9x. Giá trị của x là
A. x = 4;
B. x = 1;
C. x = 2;
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: D
Ta có G là trọng tâm của ∆ABC.
Suy ra .
Do đó .
4x + 6 = 2.3x
4x + 6 = 6x
4x – 6x = –6
–2x = –6.
x = –6 : (–2)
x = 3.
Cho ∆ABC có đường trung tuyến AD. Trên đoạn thẳng AD lấy hai điểm E, G sao cho AG = GE = ED. Trọng tâm của ∆ABC là điểm:
Cho tam giác ABC, đường trung tuyến BD. Trên tia đối của tia DB lấy điểm E sao cho DE = DB. Gọi M, N theo thứ tự là trung điểm của BC; CE. Gọi I; K theo thứ tự là giao điểm của AM, AN và BE. Khẳng định nào sau đây là đúng?
Cho tam giác ABC có đường trung tuyến AM. Gọi G là điểm thuộc tia AM sao cho AG = 2GM. Khẳng định nào sau đây là đúng?
Điền số thích hợp vào chỗ trống: “Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng … độ dài đường trung tuyến đi qua đỉnh ấy”.
Tam giác ABC có trung tuyến AM = 9 cm và G là trọng tâm. Độ dài đoạn AG là:
Cho ∆ABC có ba đường trung tuyến AX, BY, CZ cắt nhau tại G. Biết GA = GB = GC. Khẳng định nào sau đây là đúng?
Cho tam giác ABC, các đường trung tuyến BD và CE. Khẳng định nào sau đây là đúng?