Có ba chai thuỷ tinh giống nhau (khối lượng và dung tích bằng nhau) đựng các chất khí khác nhau (He, C₄H₁₀, CO₂) ở cùng nhiệt độ 20 °C và áp suất 1,913.10⁵ Pa. Các chai đựng khí được cân bằng cân điện tử. Kết quả cân được ghi trong hàng thứ 2 bảng dưới.

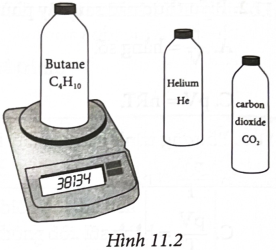
1. Tính các giá trị còn trống trong bảng, biết khối lượng của chai khi chưa chứa khí là 378,68 g

2. So sánh các số liệu tìm được trong hàng cuối. Có phải chúng ta có thể dự đoán được kết quả so sánh này không? Tại sao?

3. Hãy dùng phương trình trạng thái của khí lí tưởng để tìm lại các giá trị của n trong bảng.

Khí	He	C4H10	CO2
Kết quả cân (g)	378,86	381,34	380,70
Khối lượng khí m (g)
Khối lượng mol M (g/mol)
Số mol n

Một tàu ngầm dùng để nghiên cứu biển đang lặn ở độ sâu 100 m. Người ta mở một bình dung tích 60 lít chứa khí ở áp suất 10⁷ Pa và nhiệt độ 27 °C để đẩy nước ra khỏi thùng chứa nước ở giữa hai lớp vỏ của tàu làm cho tàu nổi lên. Sau khi dãn nở, nhiệt độ của khí là 3 °C. Tính thể tích nước bị đẩy ra khỏi tàu. Coi khối lượng riêng của nước biển là 1 000 kg/m³; gia tốc trọng trường là 9,81 m/s², áp suất khí quyển là 1,013.10⁵ Pa.

Trong hiện tượng nào sau đây cả ba thông số trạng thái của một lượng khí đều thay đổi?

Xác định khối lượng riêng của không khí trên đỉnh Fansipan cao 3 140 m trong dãy Hoàng Liên Sơn, biết mỗi khi lên cao 10 m thì áp suất khí quyển giảm 1 mmHg và nhiệt độ trên đỉnh núi này là 2 °C. Biết khối lượng riêng ở điều kiện chuẩn (0 °C và 760 mmHg) của khí quyển là 1,29 kg/m³.

Nên dùng phương trình Clapeyron để xác định các thông số trạng thái của chất khí trong trường hợp nào sau đây? Tại sao?

a) Khí trong quả bóng thám không đang bay lên cao.

b) Không khí trong quả bóng bàn bị bẹp được nhúng vào nước nóng.

c) Khí trong bọt khí đang nổi lên trong một ấm đun nước khi nước sắp sôi.

Về bóng thám không vô tuyến (Radiosonde)

Ngày nay, trong ngành khí tượng, người ta dùng bóng thám không vô tuyến có mang các thiết bị cảm biến khí tượng, thiết bị vô tuyến điện và định vị toàn cầu để thu thập và gửi về các trung tâm khí tượng ở mặt đất số liệu về nhiệt độ, áp suất, độ ẩm của khí quyển; tốc độ gió; tốc độ di chuyển của các đám mây,... Vỏ bóng được làm bằng cao su tự nhiên hoặc cao su tổng hợp từ hợp chất polychloroprene. Bóng được bơm khí H₂ hoặc He. Vỏ bóng trước khi thả có độ dày khoảng 0,051 mm và chỉ giảm xuống còn khoảng 0,0025 mm ở độ cao mà bóng bị vỡ. Tuỳ loại bóng mà khi bắt đầu thả, bóng có thể có đường kính từ 1 m đến 2 m, đến khi đạt độ cao trên 30 km thì đường kính của bóng có thể tăng lên gấp 3 lần. Bóng có thể bay lên độ cao tới 40 km, chịu được nhiệt độ tới –95 °C và thường tồn tại trên cao trong khoảng từ 1 giờ đến 3 giờ trước khi vỡ, tự động mở dù rơi xuống. Mặc dù bóng có gắn thiết bị định vị toàn cầu nhưng xác suất để tìm lại các thiết bị của bóng còn nguyên vẹn là rất nhỏ.

1. Bóng thám không chỉ có thể bay lên được trong điều kiện nào sau đây? Hãy tìm phương án trả lời chính xác nhất.

A. Khi khối lượng riêng của bóng nhỏ hơn khối lượng riêng của không khí bên ngoài.

B. Khi khối lượng riêng của khí dùng để bơm bóng nhỏ hơn khối lượng riêng của không khí bên ngoài.

C. Khi áp suất do chuyển động nhiệt của các phân tử khí trong vỏ bóng nhỏ hơn áp suất khí quyển bên ngoài.

D. Khi áp suất do chuyển động nhiệt của các phân tử khí trong vỏ bóng lớn hơn áp suất khí quyển bên ngoài.

2. Nội dung câu nào dưới đây là đúng, sai?

3. Khi bóng đang bay lên, khí trong bóng có tuân theo định luật Boyle không? Tại sao?

4. Giải thích tại sao càng bay lên cao thì thể tích của bóng càng tăng và đến một độ cao nhất định nào đó thì bóng sẽ bị vỡ.

Người ta bơm 10³ m³ không khí nóng ở nhiệt độ T = 300 K vào một khinh khí cầu. Nhiệt độ và áp suất của khí quyển lúc này là T₀ = 279 K và p₀ = 1,00 bar. Khối lượng khí cầu là 240 kg. Khi đó, khinh khí cầu chưa thể bay lên được.

a) Tính lượng không khí chứa trong khinh khí cầu. Biết muốn khí cầu bay lên chỉ cần tăng nhiệt độ của không khí trong khí cầu mà không cần bơm thêm không khí vào hoặc lấy bớt không khí ra. Coi đây là quá trình đẳng áp; nhiệt dung riêng đẳng áp của không khí là $c_{mp}=7\frac{R}{2}$ hằng số khí lí tưởng R = 8,31 J/mol.K và khối lượng mol của không khí M_A = 29 g/mol.

b) Tính thể tích của khí cầu để nó có thể bắt đầu bay lên.

c) Tính nhiệt lượng cần cung cấp cho khí cầu để đun nóng không khí.

(Trích đề thi Olimpic Vật lí Thụy Sĩ 1996)

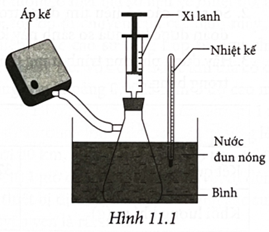
Hãy chứng tỏ rằng với dụng cụ vẽ ở Hình 11.1, người ta có thể làm thí nghiệm kiểm chứng phương trình trạng thái của một lượng khí không đổi: $\frac{pV}{T}=$hằng số.

Phương trình nào sau đây không phải là phương trình Clapeyron?

Trong SGK Vật lí của một số nước, phương trình trạng thái của khí lí tưởng được xây dựng từ phương trình của quá trình đẳng nhiệt và phương trình của quá trình đẳng tích.

1. Hãy dùng cách trên để xây dựng phương trình trạng thái của khí lí tưởng.

2. Theo em thì cách này có thể có những ưu điểm nào, nhược điểm nào so với cách dùng trong SGK của chúng ta.