Cho tam giác ABC (AC > AB), trung tuyến AM. Trên tia đối của tia MA lấy D sao cho MD = MA
a. Chứng minh ΔMAB = ΔMDC rồi suy ra AB = CD
 Giải bởi Vietjack
Giải bởi Vietjack
a. Hình vẽ (0.5 điểm)
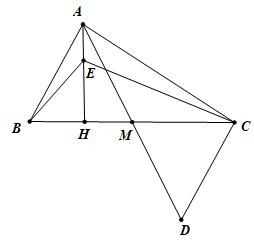
Xét ΔABM và ΔDCM có:
BM = MC
∠(AMB) = ∠(BMC)
AM = MD
⇒ ΔABM = ΔDCM (c.g.c) (0.5 điểm)
⇒ AB = DC (hai cạnh tương ứng) (0.5 điểm)
Cho tam giác ABC (AC > AB), trung tuyến AM. Trên tia đối của tia MA lấy D sao cho MD = MA.
b. Chứng minh ∠(ADC) > ∠(DAC) . Từ đó suy ra ∠(MAB) > ∠(MAC) .
Tam giác ABC có hai trung tuyến BM và CN cắt nhau tại trọng tâm G. Phát biểu nào sau đây là đúng
Cho tam giác ABC (AC > AB), trung tuyến AM. Trên tia đối của tia MA lấy D sao cho MD = MA.
c. Kẻ đường cao AH. Lấy E là một điểm nằm giữa A và H. So sánh độ dài HC và HB, EB và EC.
B. Phần tự luận (7 điểm)
Cho tam giác ABC có
a. So sánh ba góc của tam giác ABC. Tam giác ABC là tam giác gì? Vì sao
Cho tam giác ABC có
b. Vẽ đường cao AH, lấy điểm M trên AH, so sánh MB và MC
A. Phần trắc nghiệm (3 điểm)
Trong mỗi câu dưới đây, hãy chọn phương án trả lời đúng:
Khẳng định nào sau đây đúng về giao điểm của ba đường phân giác của tam giác.
Cho tam giác vuông tại A có Biết độ dài cạnh BC là một số nguyên. BC là:
Cho tam giác ABC có AC > AB, đường cao AD. Trong các khẳng định sau khẳng định nào sai?