Cho tam giác ABC (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) bằng một tam giác có ba đỉnh là O, K, H. Viết kí hiệu về sự bằng nhau của hai tam giác. Biết ?
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
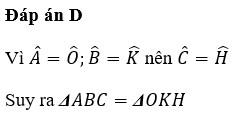
Cho tam giác ABC và tam giác MNK có: AB=MN, . Cần điều kiện gì để tam giác ABC bằng với tam giác MNK?
Cho đoạn thẳng AB, O là trung điểm của đoạn thẳng AB. Trên cùng một nửa mặt phẳng bờ AB vẽ các tia Ax, By vuông góc với AB. Gọi C là một điểm thuộc tia Ax. Đường vuông góc với OC tại O cắt tia By tại D. Khi đó
Cho tam giác ABC có . Tia phân giác góc C cắt AB tại M. Tính số các góc
Cho tam giác MNP có MN=MP. Gọi A là trung điểm của NP. Biết góc NMP bằn 40 độ thì số đo góc MPN bằng
Cho tam giác ABC = tam giác DEF. Biết . Tính các góc A, C, D, F ?
Cho góc nhọn xOy, Oz là tia phân giác của góc đó. Qua điểm A thuộc tia Ox kẻ song song với Oy cắt Oz tại M. Qua M kẻ đường song song với Ox cắt Oy tại B. Chọn câu đúng
Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C, trên tia Oy lấy hai điểm B, D sao cho OA=OB; OC=OD; (A nằm giữa O và C; B nằm giữa O và D)
Cho đoạn thẳng AB=6 cm. Trên một nửa mặt phẳng bờ AB vẽ tam giác ABC sao cho AC=4 cm, BC=5 cm, trên nửa mặt phẳng còn lại vẽ tam giác ABD sao cho BD= 4cm. Chọn đáp án đúng
Cho góc nhọn xOy. Trên tia Ox lấy hai điểm A, C, trên tia Oy lấy hai điểm B, D sao cho OA=OB; OC=OD (A nằm giữa O và C; B nằm giữa O và D). So sánh hai góc CAD và góc CBD
Cho tam giác DEF= tam giác MNP. Biết EF+FD=10 cm và NP-MP=2cm. Tính độ dài cạnh FD