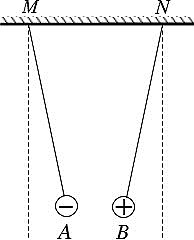
Hai quả cầu nhỏ A và B mang các điện tích lần lượt là -2.10-9C và 2.10-9C được treo ở hai đầu sợi chỉ cách điện có chiều dài như nhau, hai điểm treo M và N cách nhau 2cm. Khi các quả cầu cân bằng thì vị trí các dây treo có dạng như hình vẽ. Để đưa các dây treo trở về vị trí thẳng đứng người ta phải dùng một điện trường đều có:
A.Chiều hướng sang phải và có độ lớn 45000V/m.
B.Chiều hướng xuống dưới và có độ lớn 3600V/m.
C.Chiều hướng sang trái và có độ lớn 45000V/m.
D.Chiều hướng lên và có độ lớn 36000V/m.
 Giải bởi Vietjack
Giải bởi Vietjack
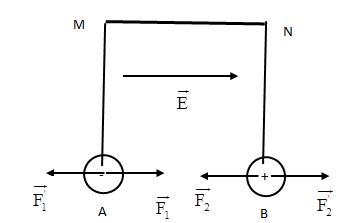
- Gọi \(\overrightarrow {{F_1}} ,\overrightarrow {\,\,{F_2}} \) là lực tương tác điện giữa hai quả cầu (phương chiều như hình vẽ)
- Để đưa các dây treo trở về vị trí thẳng đứng thì cần tác dụng các lực \(\overrightarrow {{F_1}} ,\overrightarrow {\,\,{F_2}} \) cân bằng với các lực \(\overrightarrow {{F_1}} ,\overrightarrow {\,\,{F_2}} \) (hình vẽ). Lực \(\overrightarrow {{F_1}} ,\overrightarrow {\,\,{F_2}} \) này do điện trường đều \(\overrightarrow E \)đặt thêm vào gây ra. Vì qA < 0, qB > 0 nên phải dùng một điện trường đều \(\overrightarrow E \)có chiều hướng sang phải. (hình vẽ)
- Xét sự cân bằng của quả cầu A, ta có: F1 = F'1
Với \({F_1} = \frac{{k\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}} = \frac{{{{9.10}^9}.\left| { - {{2.10}^{ - 9}}{{.2.10}^9}} \right|}}{{1.0,{{02}^2}}} = {9.10^{ - 5}}N\)
F'1 = |qA|E = 2.10-9E
Vậy độ lớn của cường độ điện trường là: \(E = \frac{{{{9.10}^{ - 5}}}}{{{{2.10}^{ - 9}}}} = 45000\left( {V/m} \right)\)
Chọn đáp án A
Bộ pin của một thiết bị điện có thể cung cấp một dòng điện 2A liên tục trong 1 giờ thì phải nạp lại. Nếu thiết bị này được bật chế độ tiết kiệm năng lượng thì bộ pin trên có thể sử dụng được liên tục trong 8 giờ mới phải nạp lại, khi đó cường độ dòng điện mà bộ pin này có thể cung cấp là:
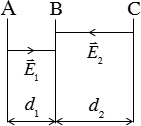
Ba bản kim loại phẳng A, B, C được tích điện và đặt song song như hình vẽ. Biết d1= 5cm, d2= 8cm, giữa các bản là điện trường đều có chiều như hình vẽ và có độ lớn E1= 4.104V/m và E2= 5.104V/m. Chọn gốc điện thế tại bản A thì điện thế của hai bản B và C lần lượt là:
A. Ba đại lượng Q, C và U liên hệ với nhau bởi biểu thức C = Q.U.
A. \(E = k\frac{{\left| Q \right|}}{{{r^2}}}\).