Cho cặp góc đối đỉnh \[\widehat {tOz}\] và \[\widehat {t'Oz'}\] (Oz và Oz’ là hai tai đối nhau). Biết \[3.\widehat {tOz'} = \widehat {tOz}\]. Tính các góc \[\widehat {tOz}\] và \[\widehat {t'Oz'}\].
A. \[\widehat {tOz} = \widehat {t'Oz'} = 45^\circ \];
B. \[\widehat {tOz} = \widehat {t'Oz'} = 105^\circ \];
C. \[\widehat {tOz} = \widehat {t'Oz'} = 135^\circ \];
D. \[\widehat {t'Oz'} = 135^\circ ,\;\widehat {tOz} = 45^\circ \].
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
Vì Oz và Oz’ là hai tai đối nhau nên ta có: \[\;\widehat {tOz} + \widehat {tOz'} = 180^\circ \] (hai góc kề bù)
Mà \[3.\widehat {tOz'} = \widehat {tOz}\]\( \Rightarrow \widehat {tOz'} = \frac{1}{3}\widehat {tOz}\)
\[\; \Rightarrow \widehat {zOt} + \frac{1}{3}\widehat {tOz} = 180^\circ \]
\[ \Rightarrow \frac{4}{3}.\widehat {zOt} = 180^\circ \Rightarrow \widehat {zOt} = 135^\circ \]
Vì \[\widehat {tOz}\] và \[\widehat {t'Oz'}\] là hai góc đối đỉnh nên \[\widehat {zOt} = \widehat {z'Ot'} = 135^\circ \]
Vậy \[\widehat {zOt} = \widehat {z'Ot'} = 135^\circ \].
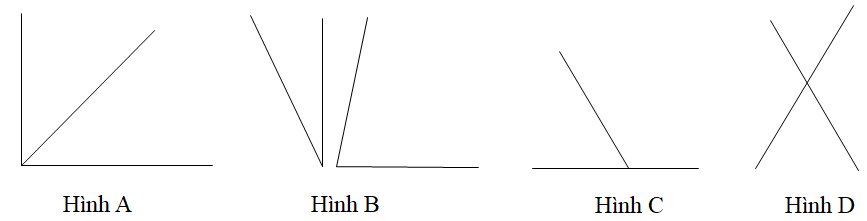
Trong các hình dưới đây hình nào vẽ hai góc kề nhau là không đúng.