Cho hai điểm phân biệt M, N. Ta vẽ một đường thẳng a đi qua điểm M và một đường thẳng b đi qua điểm N sao cho a // b. Có thể vẽ được bao nhiêu cặp đường thẳng a, b thỏa mãn điều kiện trên.
A. Một cặp;
B. Hai căp;
C. không có cặp nào;
D. Vô số cặp.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
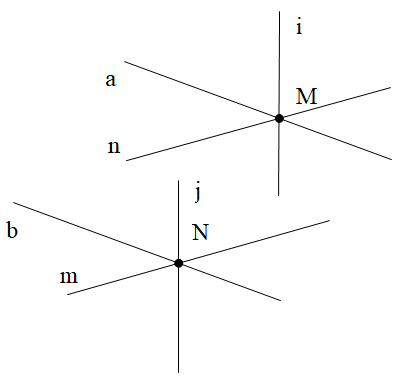
Qua một điểm M cho trước ta có thể vẽ được vô số đường thẳng (ví dụ đường thẳng a, đường thẳng n, đường thẳng i như trên hình vẽ).
Cứ tương ứng với mỗi một đường thẳng đi qua M thì ta vẽ được một đường thẳng đi qua N (theo Tiên đề Euclid) và song song với đường thẳng đó. Trên hình vẽ ta có b //a, m // n, j // i.
Vậy ta vẽ được vô số cặp đường thẳng thoả mãn yêu cầu đề bài.
Qua một điểm ở ngoài đường thẳng, ta kẻ được bao nhiêu đường thẳng song song với đường thẳng đó.
Qua điểm A nằm ngoài đường thẳng x, ta vẽ hai đường thẳng qua A và song song với x thì:
Cho hình vẽ
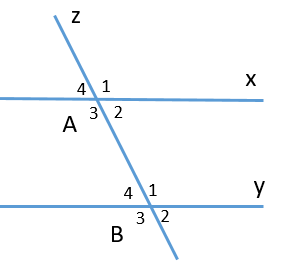
Biết một cặp góc đồng vị \[\widehat {{A_4}} = \widehat {{B_4}} = 30^\circ \]. Tính số đo của cặp góc đồng vị \[\widehat {{A_3}}\] và \[\widehat {{B_3}}\].
Cho hình vẽ
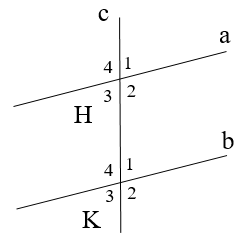
Biết \[\widehat {{K_1}} = \widehat {{H_3}} = 42^\circ .\]. Tính \[\widehat {{H_3}} + \widehat {{K_4}}\]
Trong các câu sau có bao nhiêu câu đúng?
Nếu một đường thẳng cắt hai đường thẳng song song thì:
(I) Hai góc đồng vị bằng nhau
(II) Hai góc so le trong bằng nhau
(III) Hai góc bù nhau bằng nhau
Biết một cặp góc so le trong \[\widehat {{A_2}}\; = \widehat {{B_4}} = 36^\circ \]. Tính số đo của cặp góc so le trong còn lại:

Cho hình vẽ

Biết a // b, \[\widehat {{H_3}} = 42^\circ \]. Tính số đo \[\widehat {{K_3}}\]
Cho hình vẽ dưới đây:
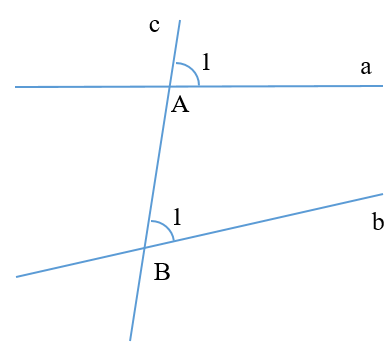
\[\widehat {{A_1}}\] và \[\widehat {{B_1}}\] là hai góc:
A. so le trong;
Nếu đường thẳng z cắt hai đường thẳng x, y và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
Cho hình vẽ
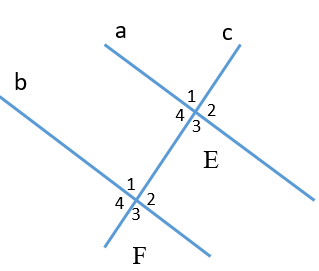
Biết a // b,
\[{\widehat E_1} = 51^\circ \]. Số đo \[\widehat {{F_3}}\] là: