Cho ∆ABC có E và D lần lượt là trung điểm của AB và BC. Từ E và D kẻ đường trung trực cắt nhau tại O. Cho F là trung điểm của AC. Khi đó:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
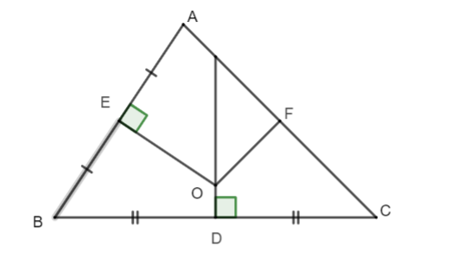
Xét ∆ABC có:
OE là đường trung trực của AB (gt);
OD là đường trung trực của BC (gt);
OE và OD cắt nhau tại O.
Do đó O là trực tâm của ∆ABC.
Mà F là trung điểm của AC.
Nên OF là đường trung trực của AC.
Vậy đáp án B và C đều đúng.
Cho tam giác ABC vuông tại A có = 60°, H là trung điểm của BC. Từ H kẻ đường vuông góc với BC cắt AC tại K. Tính .
Cho tam giác ABC có đường cao BE và trực tâm K. Gọi H là giao điểm của AK và BC. Từ C kẻ đường thẳng vuông góc với BC cắt AB tại D. Khẳng định nào sau đây là đúng?
Trong khu dân cư có ba điểm dân cư D, E, F người ta muốn xây một công viên H cách đều cả ba điểm dân cư (như hình vẽ).
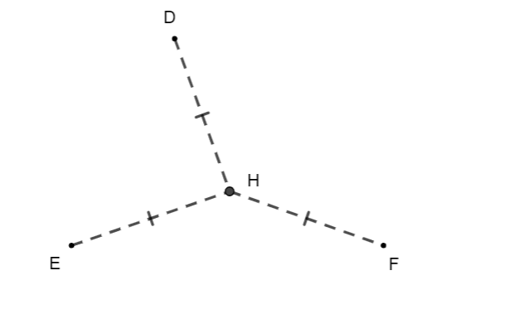
Khi đó vị trí của H là:
Cho tam giác ABC có E, F lần lượt là trung điểm của AB và BC. Cho O cách đều ba đỉnh của tam giác ABC. Khi đó:
Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau tại G. Tỉ số bằng:
Cho tam giác ∆ABC cân tại A có hai đường trung tuyến BH và CK cắt nhau tại G. Biết BG = 6 cm. Độ dài đoạn thẳng CK bằng:
Cho tam giác ∆ABC có là góc tù. Các đường trung trực của AB và AC cắt nhau tại O. Đường tròn tâm O bán kính OA đi qua điểm:
Cho tam giác ABC nhọn có đường trung trực AD với D nằm trên BC. Khi đó:
Cho tam giác ABC có hai đường trung tuyến AD và CE cắt nhau tại G. Đường thẳng BG cắt AC tại F. Cho AC = 10 cm. Độ dài đoạn thẳng AF bằng:
Cho tam giác DEF vuông tại E. Trên tia DE lấy điểm M sao sao DM = DF. Tia phân giác của góc cắt EF tại H . Khi đó:
Cho hình vẽ như bên dưới. Biết AH = 6 cm, BC = 8 cm.
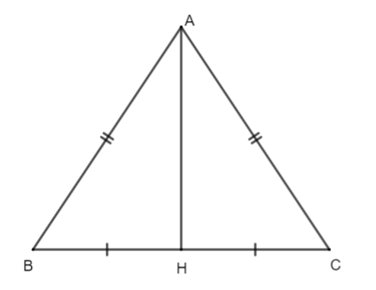
Diện tích tam giác ABC bằng:
Cho tam giác ABC có AB = 2, BC = 8 cm. Biết độ dài cạnh AC là một số nguyên tố. Chu vi tam giác ABC là: