Cho hình thang cân MNPQ như hình vẽ sau:
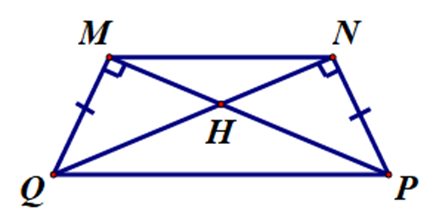
Trong hình bên có mấy cặp tam giác vuông bằng nhau?
A. 0;
B. 1;
C. 2;
D. 3.
Giải bởi Vietjack
Đáp án đúng là: C
Xét ∆MPQ và ∆NQP, có:
\[\widehat {QMP} = \widehat {PNQ} = 90^\circ \].
MQ = NP (MNPQ là hình thang cân).
PQ là cạnh chung.
Do đó ∆MPQ = ∆NQP (cạnh huyền – cạnh góc vuông).
∆MQH vuông tại M: \[\widehat {MQH} + \widehat {MHQ} = 90^\circ \] (1).
∆NPH vuông tại N: \[\widehat {NPH} + \widehat {NHP} = 90^\circ \] (2).
Ta có \[\widehat {MHQ} = \widehat {NHP}\] (2 góc đối đỉnh) (3).
Từ (1), (2), (3), ta suy ra \[\widehat {MQH} = \widehat {NPH}\].
Xét ∆MQH và ∆NPH, có:
\[\widehat {QMH} = \widehat {PNH} = 90^\circ \].
MQ = NP (giả thiết).
\[\widehat {MQH} = \widehat {NPH}\] (chứng minh trên).
Do đó ∆MQH = ∆NPH (cạnh góc vuông – góc nhọn kề).
Vậy ta có 2 cặp tam giác vuông bằng nhau là:
+ ∆MPQ = ∆NQP (cạnh huyền – cạnh góc vuông).
+ ∆MQH = ∆NPH (cạnh góc vuông – góc nhọn kề).
Ta chọn đáp án C.
Cho ∆MNP và ∆GHI có \[\widehat M = \widehat G = 90^\circ \] và NP = HI. Cần thêm điều kiện gì để ∆MNP = ∆GHI theo trường hợp cạnh huyền – góc nhọn?
Cho ∆ABC và ∆DEF có BC = EF, . Cần thêm điều kiện gì để ∆ABC = ∆DEF theo trường hợp cạnh huyền – cạnh góc vuông?
Cho tam giác ABC nhọn có AH ⊥ BC tại H. Trên tia đối của tia AB, lấy điểm D sao cho AD = AB. Kẻ DE ⊥ AH tại E. Hỏi ∆AHB = ∆AED theo trường hợp nào?
Cho ∆FDE và ∆PQR có: \[\widehat E = \widehat R = 90^\circ \], DF = QP, \[\widehat D = \widehat P = 30^\circ \]. Phát biểu nào sau đây đúng?
Cho ∆ABC vuông tại A. Lấy E ∈ BC sao cho BA = BE. Từ E dựng đường thẳng vuông góc với BC, cắt AC tại D. Hỏi ∆ABD = ∆EBD theo trường hợp nào?
Trong các phương án sau, phương án nào chứa hình có hai tam giác vuông không bằng nhau?
Cho \[\widehat {xOy}\] khác góc bẹt. Trên tia phân giác Ot của \[\widehat {xOy}\] lấy điểm A. Gọi M là trung điểm OA. Đường thẳng qua M vuông góc với OA cắt Ox, Oy theo thứ tự tại B, C. Cho các khẳng định sau:
(I). “∆OBM = ∆OCM theo trường hợp cạnh góc vuông – góc nhọn kề”.
(II). “∆OBM = ∆ABM theo trường hợp hai cạnh góc vuông.”
Chọn câu trả lời đúng.
