A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack

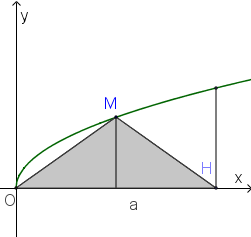
Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường và x=4 quanh trục Ox . Đường thẳng x=a(0<a<4) cắt đồ thị hàm số tại M (hình vẽ bên).