Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, SA vuông góc với mặt phẳng (ABC) và AB=2, AC=4,SA= . Mặt cầu đi qua các đỉnh của hình chóp S.ABC có bán kính là:
A. R=
B. R=5
C. R=
D. R=
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn đáp án A.
Bán kính mặt cầu ngoại tiếp tứ diện vuông S.ABC đỉnh A là:
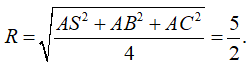
Cho tam giác ABC vuông tại A, AB=6, AC=8. Quay hình tam giác ABC xung quanh trục BC ta được một khối tròn xoay có thể tích là:
Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, tam giác SAB đều và tam giác SCD vuông cân tại S. Tính diện tích mặt cầu ngoại tiếp hình chóp.
Cho hình nón có độ dài đường sinh gấp đôi chiều cao và bán kính đáy bằng . Diện tích xung quanh của hình nón đã cho bằng:
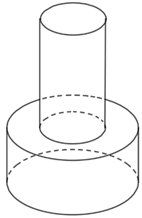
Một khối đồ chơi gồm hai khối trụ (H1),(H2) xếp chồng lên nhau, lần lượt có bán kính đáy và chiều cao tương ứng là thỏa mãn (tham khảo hình vẽ). Biết rằng thể tích của toàn bộ khối đồ chơi bằng thể tích của khối trụ (H1) bằng:
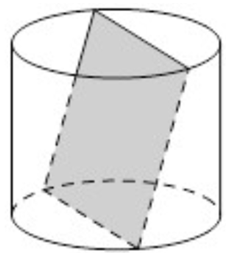
Một chiếc hộp hình trụ với bán kính đáy bằng chiều cao và bằng 10 cm. Một học sinh bỏ một miếng bìa hình vuông vào chiếc hộp đó và thấy hai cạnh đối diện của miếng bìa lần lượt là các dây cung của hai đường tròn đáy hộp và miếng bìa không song song với trục của hộp. Hỏi diện tích của miếng bìa đó bằng bao nhiêu?
Để tính diện tích xung quanh của một khối cầu bằng đá, người ta thả nó vào một chiếc thùng hình trụ có chiều cao 2m, bán kính đường tròn đáy 0,5m và có chứa sẵn một lượng nước có thể tích bằng thể tích của thùng. Sau khi thả khối cầu bằng đá vào, người ta đo được mực nước trong thùng cao gấp 3 lần mực nước ban đầu khi chưa thả khối cầu bằng đá vào. Diện tích xung quanh của khối cầu bằng đá gần nhất với kết quả nào dưới đây ?
Trong không gian cho tam giác ABC vuông tại B, BC=a, . Tính diện tích xung quanh của hình nón tạo thành khi quay tam giác ABC xung quanh trục AB.
Trong không gian, cho tam giác ABC vuông tại A có AB = 3, AC = 4. Tính diện tích toàn phần Stp của hình nón khi quay tam giác ABC xung quanh trục AC.
Hai hình nón bằng nhau có chiều cao bằng 2 dm, được đặt như hình vẽ bên (mỗi hình đều đặt thẳng đứng với đỉnh nằm phía dưới). Lúc đầu, hình nón trên chứa đầy nước và hình nón dưới không chứa nước. Sau đó, nước được chảy xuống hình nón dưới thông qua lỗ trống ở đỉnh của hình nón trên. Hãy tính chiều cao của nước trong hình nón dưới tại thời điểm khi mà chiều cao của nước trong hình nón trên bằng 1 dm.

Cho hình trụ tròn xoay có hai đáy là hai hình tròn (O;R), (O',R). Biết rằng tồn tại dây cung AB của đường tròn O sao cho O'AB là tam giác đều và (O'AB) hợp với đường tròn O một góc . Tính diện tích xung quanh của hình trụ.
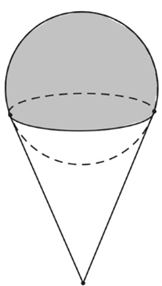
Một que kem ốc quế gồm hai phần: phần kem đóng băng có dạng hình cầu, phần ốc quế có dạng hình nón. Giả sử hình nón có bán kính đường tròn đáy bằng bán kính hình cầu. Biết rằng khi kem tan chảy hết thì sẽ làm đầy ốc quế và thể tích phần kem sau khi tan chảy bằng 75% thể tích phần kem đóng băng. Tỷ số giữa chiều cao và bán kính đường tròn đáy của hình nón bằng:
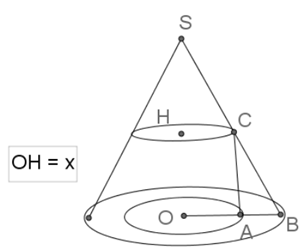
Một nóc tòa nhà cao tầng có dạng hình nón. Người ta muốn xây một bể nước có dạng một hình trụ nội tiếp trong hình nón để chứa nước (như hình vẽ minh họa). Cho biết SO=h, OB=R, OH=x ( 0<x<h). Tìm thể tích lớn nhất của hình trụ.
Cho hình chóp tứ giác đều có cạnh đáy bằng a, mặt bên tạo với mặt đáy 1 góc . Diện tích xung quanh của hình nón ngoại tiếp hình chóp là:
Cho hình chữ nhật ABCD có AB = 2AD. Quay hình chữ nhật đã cho quanh AD và AB ta được hai hình trụ tròn xoay có thể tích lần lượt là V1, V2. Mệnh đề nào dưới đây đúng?