Có bao nhiêu số phức z thỏa mãn là số thuần ảo và |z - 2i| = 1?
A. 0;
B. Vô số;
C. 1;
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
Đặt z = a + bi
Khi đó
= a + bi + ai + bi2 + a - bi = (2a - b) + ai
Để là số thuần ảo nên suy ra
2a - b = 0 Û b = 2a
Khi đó z = a + 2ai
+) |z - 2i| = 1
Û a2 + (2a - 2)2 = 1
Û 5a2 - 8a + 3 = 0
Û 5a2 - 5a - 3a + 3 = 0
Û 5a(a - 1) - 3(a - 1) = 0
Û (5a - 3)(a - 1) = 0
Vậy có 2 số phức z thỏa mãn là và z = 1 + 2i.
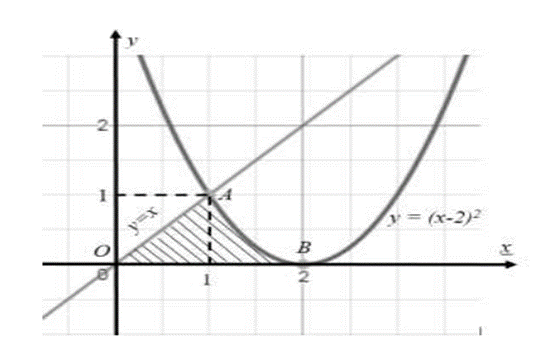
Tính diện tích phần hình phẳng gạch chéo (tam giác cong OAB) trong hình vẽ bên.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1; 0; 2) và B(4; 1; 1) Vectơ có tọa độ là:
Trong không gian Oxyz. Điểm nào sau đây thuộc mặt phẳng (P): -2x + y - 5 = 0?
Cho hàm số y = f (x) liên tục trên đoạn [a; b]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f (x), trục hoành và hai đường thẳng x = a, x = b (a < b). Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức:
Cho hàm số f (x) liên tục trên [a; b] và F (x) là một nguyên hàm của f (x). Tìm khẳng định sai.
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = 2(x - 1)ex, trục tung và trục hoành. Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox
Trong không gian Oxyz, cho ba điểm M(1; 3; 2), N(-1; 2; 1), P(1; 2; -1). Lập phương trình tham số của đường thẳng đi qua điểm M và song song với NP.