Trong không gian Oxyz, cho hai mặt phẳng: (P): 5x - 3y + 2z - 19 = 0, (Q): x - y + z - 3 = 0. Tìm phương trình đường thẳng ∆ là giao tuyến của hai mặt phẳng (P), (Q).
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
+) và
Đường thẳng ∆ là giao tuyến của hai mặt phẳng (P), (Q) nên suy ra véc-tơ pháp tuyến của (P) và (Q) đều vuông góc với véc-tơ chỉ phương của ∆
= (-1; -3; -2) = -(1; 3; 2)
+) Tập hợp giao điểm của (P) và (Q) là nghiệm của phương tình
5x - 3y + 2z - 19 = x - y + z - 3
Û 4x - 2y + z - 16 = 0
Chọn M(5; 2; 0) là một giao điểm bất kỳ
Phương tình đường thẳng D đi qua M và có véc-tơ chỉ phương là (1; 3; 2)
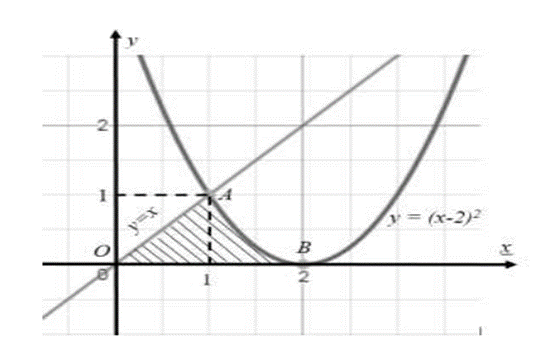
Tính diện tích phần hình phẳng gạch chéo (tam giác cong OAB) trong hình vẽ bên.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1; 0; 2) và B(4; 1; 1) Vectơ có tọa độ là:
Trong không gian Oxyz. Điểm nào sau đây thuộc mặt phẳng (P): -2x + y - 5 = 0?
Cho hàm số y = f (x) liên tục trên đoạn [a; b]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f (x), trục hoành và hai đường thẳng x = a, x = b (a < b). Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức:
Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y = 2(x - 1)ex, trục tung và trục hoành. Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục Ox
Cho hàm số f (x) liên tục trên [a; b] và F (x) là một nguyên hàm của f (x). Tìm khẳng định sai.
Trong mặt phẳng phức Oxy, gọi M là điểm biểu diễn số phức z = 4 - 3i. Tính độ dài đoạn thẳng OM.