Cho hai số phức z1, z2, thỏa mãn |z1 + 6| = 5, |z2 + 2 - 3i| = |z2 - 2 - 6i|. Giá trị nhỏ nhất của |z1 - z2| bằng
A.
B.
C.
D.
Giải bởi Vietjack
Đáp án đúng là: C
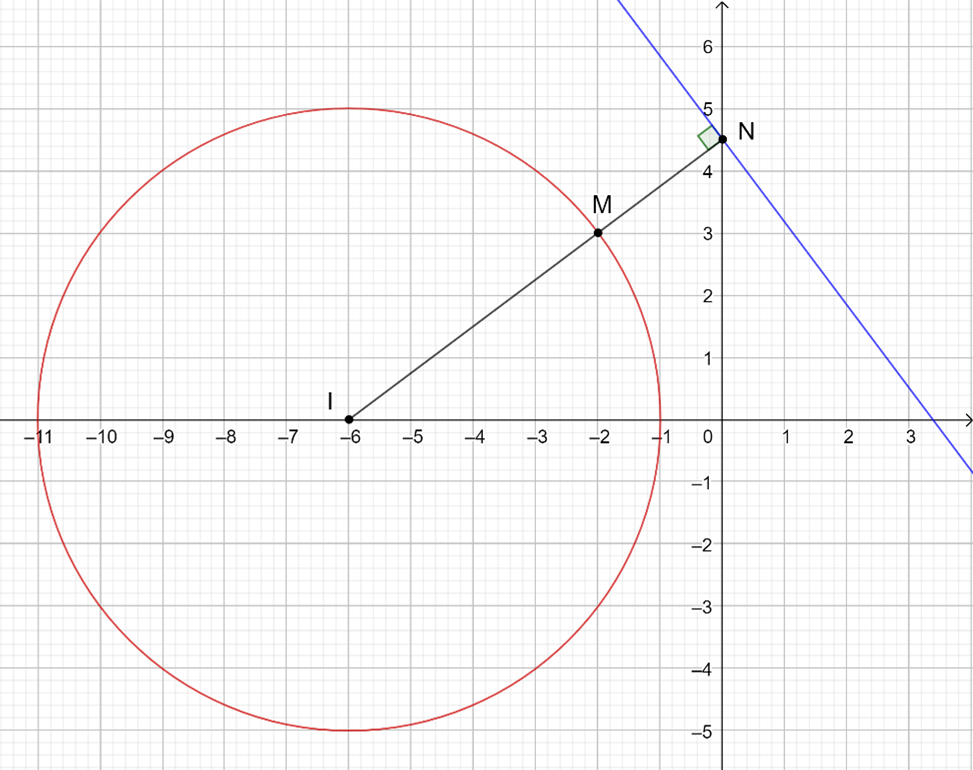
+) |z1 + 6| = 5
Û (x1 + 6)2 + y12 = 25
M(x1; y1) là điểm biểu diễn của số phức z1 và thuộc đường tròn tâm I(-6; 0) có bán kính R = 5
+) |z2 + 2 - 3i| = |z2 - 2 - 6i|
Û (x2 + 2)2 + (y2 - 3)2 = (x2 - 2)2 + (y2 - 6)2
Û x22 + 4x2 + 4 + y22 - 6y2 + 9 = x22 - 4x2 + 4 + y22 - 12y2 + 36
Û 8x2 + 6y2 - 27 = 0
N(x2; y2) là điểm biểu diễn của số phức z2 và thuộc đường thẳng 8x + 6y - 27 = 0
Ta có |z1 - z2| bằng MN và để |z1 - z2| đạt GTNN thì MN nhỏ nhất
Khi đó đường thẳng MN đi qua I, vuông góc với đường thẳng trên và M gần N nhất
Theo hình vẽ
MNmin = IN - IM
Với và IM = R = 5
Nên suy ra
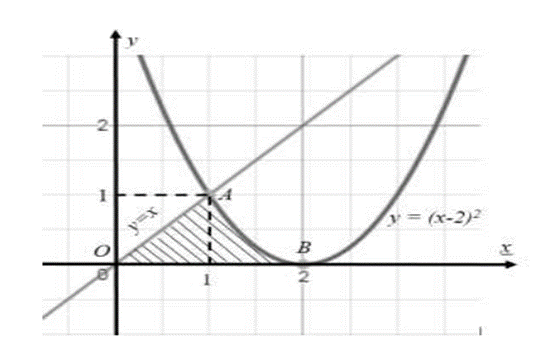
Tính diện tích phần hình phẳng gạch chéo (tam giác cong OAB) trong hình vẽ bên.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1; 0; 2) và B(4; 1; 1) Vectơ có tọa độ là:
Cho hàm số y = f (x) liên tục trên đoạn [a; b]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f (x), trục hoành và hai đường thẳng x = a, x = b (a < b). Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức:
Trong không gian Oxyz. Điểm nào sau đây thuộc mặt phẳng (P): -2x + y - 5 = 0?
Cho hàm số f (x) liên tục trên [a; b] và F (x) là một nguyên hàm của f (x). Tìm khẳng định sai.
Trong không gian Oxyz, cho mặt phẳng (P) có phương trình 3x + 2y + z + 1 = 0. Tìm một vectơ pháp tuyến của (P).
