Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thang vuông \(\left( {\widehat A = \widehat B = 90^\circ } \right).\) Có bao nhiêu góc vuông tại đỉnh A thuộc các mặt của lăng trụ?
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
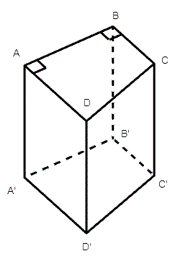
Do ABCD là hình thang vuông \(\left( {\widehat A = \widehat B = 90^\circ } \right)\) nên ta có \(\widehat {BAD} = 90^\circ .\)
Mặt khác ta có hình lăng trụ đứng ABCD.A'B'C'D' nên ta có: \(\widehat {A'AD} = 90^\circ ,\) \(\widehat {BAA'} = 90^\circ \).
Vậy có ba góc vuông tại đỉnh A thuộc các mặt của lăng trụ đứng là \(\widehat {BAD},\)\(\widehat {A'AD},\) \(\widehat {BAA'}.\)
Một hình lăng trụ đứng có tất cả 5 mặt. Hình lăng trụ này có bao nhiêu đỉnh?
Hình lăng trụ đứng tứ giác có:
(1) Các mặt đáy song song với nhau;
(2) Các mặt đáy là tam giác;
(3) Các mặt đáy là tứ giác;
(4) Các mặt bên là hình chữ nhật.
Có bao nhiêu khẳng định đúng trong các khẳng định trên?
Cho một hình lăng trụ đứng có tổng 12 cạnh. Hỏi đáy của hình lăng trụ đứng này không thể là hình gì?
Cho lăng trụ đứng tứ giác ABCD.EFGH, biết CD = 4 cm và diện tích của mặt CDHG bằng 36 cm2. Chiều cao của lăng trụ là:
Cho hình lăng trụ đứng sau:
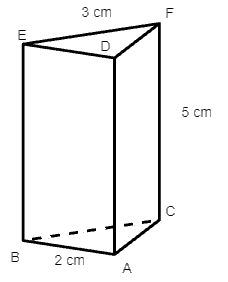
Độ dài của các cạnh ED, BC, DA lần lượt bằng
Cho hình lăng trụ đứng ABCD.EHGF có đáy ABCD là hình thang cân (AB // CD). Có bao nhiêu cạnh có độ dài bằng với độ dài cạnh GH?