Hình 4.13 có và Ax // Bm. Chứng tỏ rằng Ay // Bn.
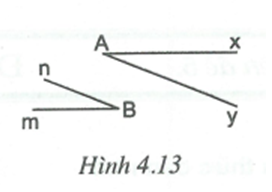
 Giải bởi Vietjack
Giải bởi Vietjack
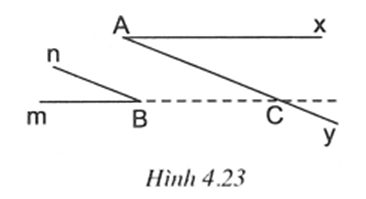
Gọi C là giao điểm của hai đường thẳng Ay và Bm.
Ta có Ax//Bm nên (cặp góc so le trong).
Mặt khác, nên .
Do đó Ay // Bn (vì có cặp góc đồng vị bằng nhau).
Cho tam giác ABC. Vẽ điểm M sao cho góc BAM bằng và so le trong với góc B. Vẽ điểm N sao góc CAN bằng và so le trong với góc C. Chứng tỏ rằng ba điểm M, A, N thẳng hàng.
Cho tam giác ABC. Từ điểm M trên cạnh BC vẽ MD//AB, ME//AC. Xác định vị trí của điểm M để tia MA là tia phân giác của góc DME.
Cho điểm O ở ngoài đường thẳng xy. Qua O vẽ n đường thẳng. Xác định giá trị nhỏ nhất của n để trong số các đường thẳng đã vẽ, ít nhất cũng có 10 đường thẳng cắt xy.
Cho tam giác ABC. Từ điểm D trên cạnh BC vẽ DE // AB; DF // AC.
a) Kể tên những góc ở trong hình vẽ bằng góc A;
Qua điểm A ở ngoài đường thẳng a vẽ 101 đường thẳng. Chứng tỏ rằng ít nhất cũng có 100 đường thẳng cắt a.
Hình 4.11 có ABAC, CD và OE . Biết ; . Tìm giá trị m để tia OE là tia phân giác của góc AOC.