Cho tam giác ABC vuông cân đáy BC. Gọi M, N là trung điểm của AB, AC. Kẻ tại H, kẻ tại E. Chứng minh rằng:
 Giải bởi Vietjack
Giải bởi Vietjack
a)
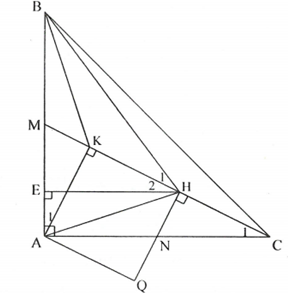
Từ A kẻ tại K và tại Q.
Hai tam giác vuông MAK và NCH có
(cùng phụ với góc AMC)
(1)
và có AK = CH, , AB = CA
và có AN = NC,
(2)
Từ (1) và (2), suy ra: AK = AQ.
và có chung
là tia phân giác của góc KHQ
Từ
Tam giác AKH có nên nó vuông cân tại K suy ra KA = KH.
hay cân tại B.
Cho tam giác ABC có M là trung điểm của BC, AM là tia phân giác góc A. Kẻ MH vuông góc với AB; MK vuông góc với AC. Chứng minh rằng: a,
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm D sao cho BD= BA . Qua D vẽ đường thẳng vuông góc với BC cắt AC tại E.
a) Chứng minh rằng:.
Cho tam giác ABC (AB < AC), M là trung điểm của BC. Đường trung trực của BC cắt tia phân giác của góc BAC tại điểm P. Vẽ PH và PK lần lượt vuông góc với đường thẳng AB và đường thẳng AC.
a) Chứng minh PB = PC và BH = CK.
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE. Kẻ tại H, kẻ tại K.
Chứng minh rằng: a,
Cho tam giác ABC cân tại A. Trên cạnh BC lấy D, E (D nằm giữa B và E) sao choBD=CE. Vẽ tại M, tại N. Gọi K là giao điểm của MD và NE. Chứng minh rằng:
a,
Cho tam giác ABC có và M là trung điểm của BC. Trên tia đối của tia CB lấy điểm D. Kẻ BK vuông góc với đường thẳng AD tại K.
Chứng minh rằng KM là tia phân giác của .