Cho tam giác ABC nhọn có đường cao AM và BN cắt nhau tại I. Gọi H là giao điểm của CI và AB. Chọn khẳng định đúng?
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
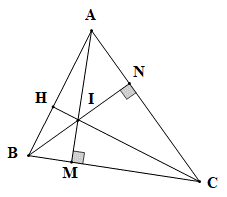
Xét DABC có hai đường cao AM và BN cắt nhau tại I nên I là trực tâm tam giác ABC.
Suy ra CI là đường cao của tam giác ABC hay CI ⊥ AB.
Do đó phương án A là đúng.
Vậy ta chọn phương án A.
Cho các hình vẽ sau:
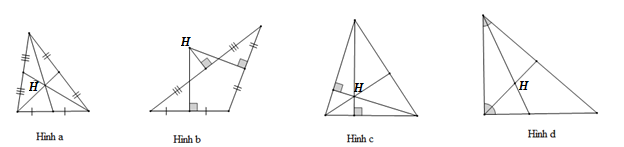
Trong các hình trên, điểm H trong hình nào là trực tâm của tam giác?
Cho các phát biểu sau:
(I) Tam giác nhọn có trực tâm nằm bên trong tam giác;
(II) Tam giác tù có trực tâm nằm bên ngoài tam giác;
(III) Tam giác vuông có trực tâm trùng với đỉnh góc vuông;
Chọn khẳng định đúng: