Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt BC ở K. Từ B kẻ đường thẳng vuông góc với AK tại H và cắt AC ở D. Chọn câu sai.
A. HB = HD;
B. HD = AB;
C. AB = AD;
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
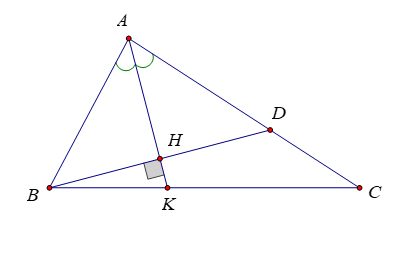
Xét ∆ABH và ∆ADH có
(vì AK là tia phân giác của góc A)
AH là cạnh chung
(vì AH ⊥ BD)
Suy ra ∆ABH = ∆ADH (g.c.g)
Do đó: HB = HD; AB = AD (2 cạnh tương ứng)
(2 góc tương ứng)
Vậy HD = AB là sai.
Cho góc nhọn xOy, Oz là tia phân giác của góc đó. Qua điểm A thuộc tia Ox kẻ song song với Oy cắt Oz tại M. Qua M kẻ đường song song với Ox cắt Oy tại B. Chọn câu đúng.
Cho tứ giác ABCD, AB // DC, AD // BC, O là giao của AC và BD. Câu nào sau đây đúng?
Cho tam giác ABC có M là trung điểm cạnh BC. Kẻ tia Ax đi qua M. Qua B, C lần lượt kẻ các đường thẳng vuông góc với Ax, cắt Ax tại H và K. So sánh BH và CK
Cho góc xOy khác góc bẹt. Trên tia phân giác của góc xOy lấy điểm I tùy ý, qua I vẽ đường thẳng vuông góc với OI cắt Ox ở E và cắt Oy ở F. Trong các khẳng định sau, khẳng định nào đúng?