Cho ∆ABC đều. lấy các điểm D, E, F lần lượt trên các cạnh AB, BC, CA sao cho AD = BE = CF.
Nhận định nào dưới đây đúng?
A. ∆DEF vuông;
B. ∆DEF vuông cân;
C. ∆DEF đều;
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
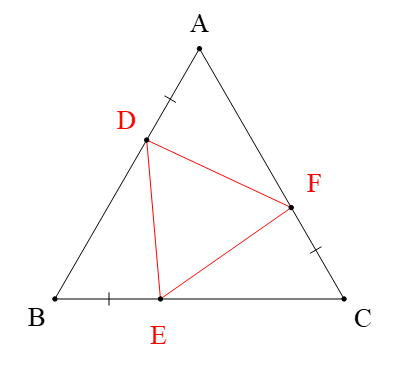
Ta có: ∆ABC đều (giả thiết) ⇒ AB = AC = BC và (tính chất)
Có AD + BD = AB; BE + EC = BC; CF + FA = AC
Mà AD = BE = CÂU: (giả thiết)
Nên BD = EC = FA
Xét ∆ADF và ∆BED có
AD = BE
FA = BD
Suy ra ∆ADF = ∆BED (c.g.c)
Do đó DF = ED (hai cạnh tương ứng) (1)
Xét ∆ADF và ∆CFE có
AD = CF
FA = EC
Suy ra ∆ADF = ∆ CFE (c.g.c)
Do đó DF = FE (hai cạnh tương ứng) (1)
Từ (1) và (2) suy ra DF = FE = ED
Do đó tam giác DFE đều.
Cho ∆ABC cân tại A. Tia phân giác của góc B và góc C cắt cạnh AC, AB lần lượt ở D và E. Đoạn thẳng có độ dài bằng đoạn thẳng BE là
Cho ∆ABC cân tại A. Tia phân giác cắt BC tại M. Đường thẳng qua M và vuông góc với AB cắt AB tại H. Đường thẳng qua M và vuông góc với AC cắt AC tại K.
Nhận định nào dưới đây sai?
