Góc giữa hai đường thẳng a: 6x – 5y + 15 = 0 và b: \(\left\{ \begin{array}{l}x = 10 - 6t\\y = 1 + 5t\end{array} \right.\) bằng
A. 30°;
B. 90°;
C. 60°;
D. 45°.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Đường thẳng a có một vectơ pháp tuyến là \(\overrightarrow {{n_1}} = \left( {6;\,\, - 5} \right)\);
Đường thẳng b có một vectơ chỉ phương là \(\overrightarrow {{u_2}} = \left( { - 6;\,\,5} \right)\) nên nó có một vectơ pháp tuyến là \(\overrightarrow {{n_2}} = \left( {5;\,6} \right)\).
Ta thấy: \(\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} = 6 \cdot 5 + \left( { - 5} \right) \cdot 6 = 0\).
Suy ra góc giữa hai đường thẳng bằng 90°.
Cho tam thức bậc hai f(x) = ax2 + bx + c, (a ≠ 0) và ∆ = b2 – 4ac. Mệnh đề nào sau đây đúng?
Viết phương trình tổng quát của đường thẳng
đi qua M(– 1; – 4) và song song với đường thẳng 3x + 5y – 2 = 0;
Gọi S là tập nghiệm của bất phương trình x2 – 8x + 7 ≥ 0. Tromg các tập hợp sau, tập nào không là tập con của S?
Cho phương trình \(\sqrt { - {x^2} + 4x - 3} = \sqrt {2m + 3x - {x^2}} \) (1). Để phương trình (1) có nghiệm thì m ∈ [a; b]. Giá trị a2 + b2 bằng
Cho hàm số bậc hai có bảng biến thiên như sau:
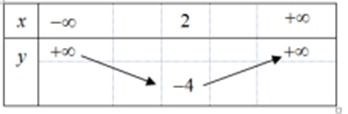
Công thức hàm số bậc hai trên là
Phương trình đường tròn đường kính AB với A(1; 3) và B(5; – 1) là
Trong các công thức sau, công thức nào không biểu diễn y là hàm số của x?
Cho đồ thị hàm số bậc hai y = ax2 + bx + c (a ≠ 0) như hình vẽ sau.
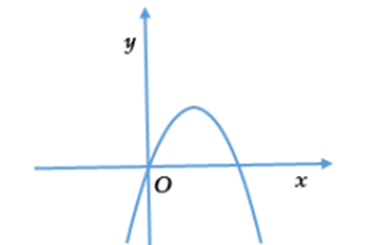
Điều kiện của hệ số a của hàm số bậc hai này là
Cho hàm số y = f(x) có đồ thị như hình dưới.
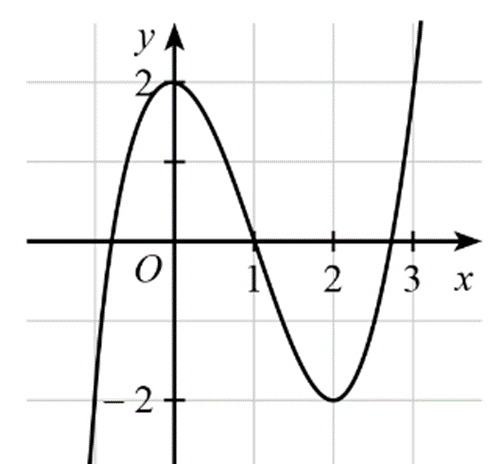
Hàm số trên nghịch biến trên khoảng
Trong mặt phẳng tọa độ, cho đường tròn (C): x2 + y2 – 2x – 4y – 4 = 0 và điểm A(1; 5). Tiếp tuyến của đường tròn (C) tại điểm A có phương trình là
Cho hàm số bậc hai f(x) = – 2x2 – x + 1. Giá trị lớn nhất của hàm số là
Cho hàm số \(y = \left\{ \begin{array}{l}{x^2} - 2023\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,x = 0\\1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x\, > 0\end{array} \right.\). Giá trị của hàm số tại x = 5 là