Cho tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\). Chứng minh rằng \(\frac{{ab}}{{cd}} = \frac{{{a^2} - {b^2}}}{{{c^2} - {d^2}}}\).
Giải bởi Vietjack
Vì \(\frac{a}{b} = \frac{c}{d}\) nên ad = bc.
Ta có: ab(c2 – d2) = abc2 – abd2 = acbc – adbd;
cd(a2 – b2) = cda2 – cdb2 = acad – bcbd.
Do đó ab(c2 – d2) = cd(a2 – b2).
Suy ra \(\frac{{ab}}{{cd}} = \frac{{{a^2} - {b^2}}}{{{c^2} - {d^2}}}\) (đpcm).
Ba đơn vị cùng vận chuyển 700 tấn hàng. Đơn vị A có 10 xe trọng tải mỗi xe là 5 tấn; đơn vị B có 20 xe trọng tải mỗi xe là 4 tấn; đơn vị C có 14 xe trọng tải mỗi xe là 5 tấn. Hỏi mỗi đơn vị vận chuyển được bao nhiêu tấn hàng, biết mỗi xe đều chở một số chuyến như nhau?
Tỉ lệ thức nào sau đây không được lập từ tỉ lệ thức \(\frac{{14}}{8} = \frac{{21}}{{12}}\)?
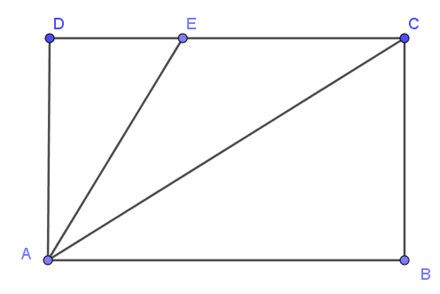
Cho ABCD là hình chữ nhật như hình vẽ, điểm E nằm trên cạnh CD. Khẳng định nào sau đây là sai?
Cho biết y tỉ lệ nghịch với x theo hệ số tỉ lệ a và khi x = –2 thì y = 4. Khi đó, hệ số a bằng bao nhiêu?
Biết đại lượng y tỉ lệ thuận với đại lượng x với các cặp giá trị tương ứng trong bảng sau:
|
x |
−5 |
1 |
|
y |
1 |
? |
Giá trị cần điền vào “?” là
\(\frac{{ - 6}}{x} = \frac{9}{{ - 15}}\);
Cho góc xOy khác góc bẹt có Ot là tia phân giác. Qua điểm H thuộc tia Ot, kẻ đường vuông góc với Ot và cắt Ox và Oy theo thứ tự A và B.
Chứng minh OA = OB.
Cho góc xOy khác góc bẹt có Ot là tia phân giác. Qua điểm H thuộc tia Ot, kẻ đường vuông góc với Ot và cắt Ox và Oy theo thứ tự A và B.
Lấy điểm C nằm giữa O và H. Chứng minh \(\widehat {ACH} = \widehat {HCB}\).
\(\frac{{3x - 7}}{8} = \frac{5}{2}\)
\(\frac{{ - 4}}{x} = \frac{x}{{ - 49}}\)
Điền vào chỗ trống sau: “Đường thẳng vuông góc với một đoạn thẳng tại … của nó được gọi là đường trung trực của đoạn thẳng đó”.
