Cho tam giác ABC vuông tại A, đường phân giác BD (D ∈ AC). Từ D kẻ DH vuông góc với BC.
a) Chứng minh ΔABD = ΔHBD.
b) So sánh AD và DC.
c) Gọi K là giao điểm của đường thẳng AB và DH, I là trung điểm của KC. Chứng minh 3 điểm B, D, I thẳng hàng.
 Giải bởi Vietjack
Giải bởi Vietjack
Giải:
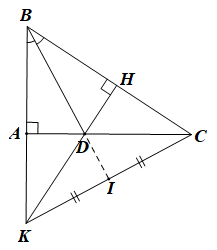
a) Xét DABD và ΔHBD có:
\(\widehat {BAD} = \widehat {BHD} = 90^\circ \),
BD là cạnh chung,
\(\widehat {ABD} = \widehat {HBD}\) (do BD là tia phân giác của \(\widehat {ABD}\)).
Do đó DABD = ΔHBD (cạnh huyền – góc nhọn).
b) Từ DABD = ΔHBD (câu a) suy ra AD = HD (hai cạnh tương ứng)
Xét DDHC vuông tại H có DC là cạnh huyền nên DC là cạnh lớn nhất
Do đó DC > HD nên DC > AD.
c) Xét DBKC có CA ⊥ BK, KH ⊥ BC và CA cắt KH tại D
Do đó D là trực tâm của DBKC, nên BD ⊥ KC (1)
Gọi J là giao điểm của BD và KC.
Xét DBKJ và DBCJ có:
\(\widehat {BJK} = \widehat {BJC} = 90^\circ \),
BJ là cạnh chung,
\(\widehat {KBJ} = \widehat {CBJ}\) (do BJ là tia phân giác của \(\widehat {ABD}\)).
Do đó DBKJ = DBCJ (cạnh góc vuông – góc nhọn kề)
Suy ra KJ = CJ (hai cạnh tương ứng)
Hay J là trung điểm của KC.
Mà theo bài I là trung điểm của KC nên I và J trùng nhau.
Do đó ba điểm B, D, I thẳng hàng.
Cho đa thức A(x) = –11x5 + 4x – 12x2 + 11x5 + 13x2 – 7x + 2.
a) Thu gọn, sắp xếp đa thức A(x) theo số mũ giảm dần của biến rồi tìm bậc, hệ số cao nhất của đa thức.
b) Tìm đa thức M(x) sao cho M(x) = A(x).B(x), biết B(x) = x – 1.
c) Tìm nghiệm của đa thức A(x).
Chọn ngẫu nhiên một số trong tập hợp M = {2; 3; 5; 6; 8; 9}.
a) Trong các biến cố sau, biến cố nào là biến cố chắc chắn? Biến cố nào là biến cố không thể và biến cố nào là biến cố ngẫu nhiên?
A: “Số được chọn là số nguyên tố”;
B: “Số được chọn là số có một chữ số”;
C: “Số được chọn là số tròn chục”.
b) Tính xác suất của biến cố A.
Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:
Từ đẳng thức 2.15 = 6.5 lập được tỉ lệ thức nào sau đây?
Giá trị nào của x thỏa mãn \[\frac{{x - 1}}{6} = \frac{{x - 5}}{7}\]?
Cho hai biểu thức: E = 2(a + b) – 4a + 3 và F = 5b – (a – b).
Khi a = 5 và b = –1. Chọn khẳng định đúng: