Trong không gian Oxyz. Cho điểm E(1,1,1), mặt cầu và mặt phẳng . Gọi là đường thẳng đi qua E, nằm trong và cắt tại hai điểm sao cho là tam giác đều. Phương trình tham số của là
A. .
 Giải bởi Vietjack
Giải bởi Vietjack
Gọi là một vectơ chỉ phương của với .
Ta có .
Vì nên .(1)
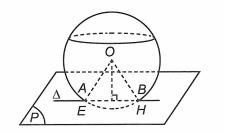
Mặt cầu có tâm và bán kính .
Gọi H là hình chiếu vuông góc của O trên AB
Ta có là tam giác đều cạnh R nên .
Suy ra khoảng cách từ O đến đường thẳng bằng .
Khi đó
(2)
Thay (1) vào (2) ta được:
Thay thì và .
Ta được một vectơ chỉ phương của là
Vậy phương trình của đường thẳng là .
Chọn C.
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(2,1,-2), B(5,1,1) và mặt cầu (S) có phương trình . Xét đường thẳng d đi qua A và tiếp xúc với (S) sao cho khoảng cách từ B đến d nhỏ nhất. Phương trình của đường thẳng d là
Đường thẳng là giao tuyến của hai mặt phẳng x+z-5=0 và x-2y-z+3=0 thì có phương trình là
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và mặt phẳng . Viết phương trình đường thẳng d' là hình chiếu vuông góc của đường thẳng d trên mặt phẳng (P).
Trong không gian Oxyz, cho hai đường thẳng và điểm . Đường thẳng đi qua điểm A, vuông góc với và cắt có phương trình là
Trong không gian với hệ tọa độ Oxyz, cho . Tìm một vectơ chỉ phương của đường thẳng AB.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P):2x-y+z-10=0, điểm A(1,3,2) và đường thẳng .
Tìm phương trình đường thẳng cắt và d lần lượt tại M và N sao cho A là trung điểm của MN.
Trong không gian Oxyz, gọi d là đường thẳng đi qua điểm A(1,-1,2), song song với mặt phẳng , đồng thời tạo với đường thẳng một góc lớn nhất. Phương trình đường thẳng d là
Trong không gian Oxyz, phương trình chính tắc của đường thẳng đi qua điểm M(2,-1,3) và có vectơ chỉ phương là
Trong không gian Oxyz, cho mặt phẳng và đường thẳng . Phương trình của đường thẳng d nằm trong mặt phẳng , cắt và vuông góc với đường thẳng là
Cho điểm A(1,2,3) và hai mặt phẳng .
Phương trình đường thẳng d đi qua A song song với cả (P) và (Q) là
Trong không gian Oxyz, cho đường thẳng vuông góc với mặt phẳng có phương trình . Một vectơ chỉ phương của là:
Trong không gian Oxyz, cho hai đường thẳng . Phương trình đường thẳng cắt lần lượt tại A và B sao cho AB nhỏ nhất là
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có . Phương trình đường cao của tam giác ABC kẻ từ đỉnh B là
Trong không gian Oxyz, cho tam giác ABC có A(2,3,3), phương trình đường trung tuyến kẻ từ B là , phương trình đường phân giác trong của góc C là .
Đường thẳng AB có một vectơ chỉ phương là