Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
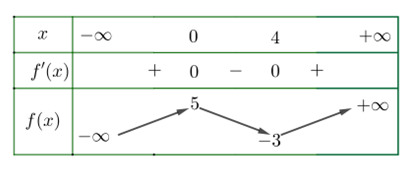
 Giải bởi Vietjack
Giải bởi Vietjack
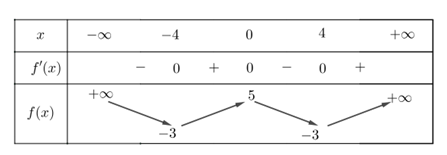
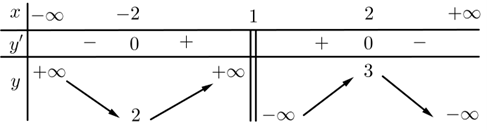
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) và có bảng xét dấu đạo hàm \(f'\left( x \right)\) như hình sau:
