Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
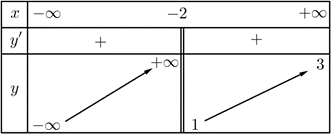
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là:
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
Chọn D
Ta có \(\mathop {\lim }\limits_{x \to \, + \infty } y = 3 \Rightarrow \) Đồ thị hàm số có tiệm cận ngang \(y = 3\).
\(\mathop {\lim }\limits_{x \to \,{{\left( { - 2} \right)}^ - }} y = + \infty \Rightarrow \) Đồ thị hàm số có tiệm cận đứng \(x = - 2\).
Vậy đồ thị hàm số có \(2\) đường tiệm cận.
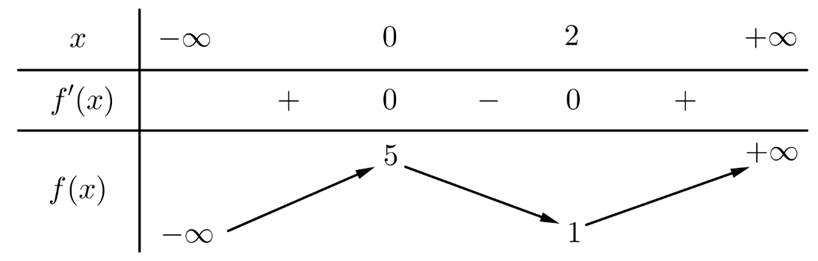
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu đạo hàm như sau:

Hàm số \(y = 3f\left( {x + 3} \right) - {x^3} + 12x\) nghịch biến trên khoảng nào sau đây?