Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng \({60^0}\). Thể tích khối chóp là
D. \(\frac{{\sqrt 2 {a^3}}}{6}\)
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Phương pháp:
* Xác định góc giữa đường thẳng và mặt phẳng:
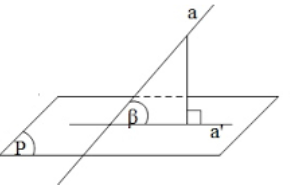
- Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).
- Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.
Cách giải:
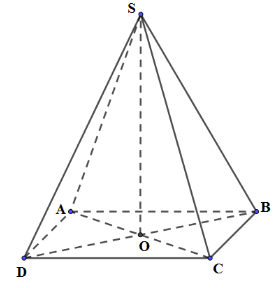
Ta có: \(SO \bot \left( {ABCD} \right) \Rightarrow \left( {SA;\left( {ABCD} \right)} \right) = \left( {SA;AO} \right) = SAO = {60^0}\)
ABCD là hình vuông cạnh a \( \Rightarrow \left\{ \begin{array}{l}{S_{ABCD}} = {a^2}\\AC = a\sqrt 2 \Rightarrow OA = \frac{{AC}}{2} = \frac{a}{{\sqrt 2 }}\end{array} \right.\)
\(\Delta SOA\) vuông tại O \( \Rightarrow SO = OA.\tan SAO = \frac{a}{{\sqrt 2 }}.\tan {60^0} = \frac{{a\sqrt 3 }}{{\sqrt 2 }}\)
Thể tích của khối chóp là: \(V = \frac{1}{3}.SO.{S_{ABCD}} = \frac{1}{3}.\frac{{a\sqrt 3 }}{{\sqrt 2 }}.{a^2} = \frac{{\sqrt 6 {a^3}}}{6}\)
Cho x, y là hai số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là sai?
Một người lần đầu gửi vào ngân hàng 100 triệu đồng với kì hạn 3 tháng, lãi suất 2% một quý theo hình thức lãi kép (một quý bằng 3 tháng). Sau đúng 6 tháng, người đó gửi thêm 100 triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được tính từ lần gửi ban đầu đến thời điểm sau khi gửi thêm 1 năm, gần nhất với kết quả nào sau đây?
Các hình trụ tròn xoay có diện tích toàn phần là S không đổi, gọi chiều cao hình trụ là h và bán kính đáy hình trụ là r. Thể tích của khối trụ đó đạt giá trị lớn nhất khi
Giá trị của m để hàm số \(y = {x^3} - 3m{x^2} + 3\left( {{m^2} - 1} \right)x + m\) đạt cực đại tại \(x = 1\) là:
Phương trình tiếp tuyến của đồ thị hàm số \(y = {x^4} - 6{x^2} + 8x - 2\) tại điểm \({x_0} = 1\) là
Cho x là số thực dương. Dạng lũy thừa với số mũ hữu tỉ của biểu thức \(\sqrt {x.\sqrt[3]{x}} \) là:
Cho hình nón có bán kính đáy bằng a, đường sinh có độ dài bằng \(a\sqrt 3 \). Thể tích của khối nón đó là
Tập hợp tất cả các số thực m để hàm số \(y = {x^3} + 5{x^2} - 4mx - 3\) đồng biến trên R là
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên là
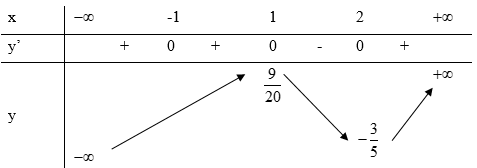
Khẳng định nào sau đây là khẳng định đúng?
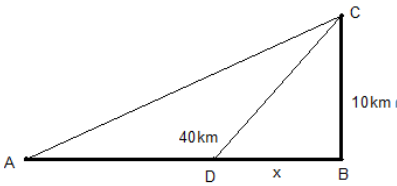
Một người cần đi từ khách sạn A bên bờ biển đến hòn đảo C. Biết rằng khoảng cách từ đảo C đến bờ biển là BC = 10km, khoảng cách từ khách sạn A đến điểm ngắn nhất tính từ đảo C vào bờ là AB = 40km. Người đó có thể đi đường thủy hoặc đi đường bộ rồi đi đường thủy từ khách sạn ra đảo (như hình vẽ dưới đây). Biết kinh phí đi đường thủy là 5 USD/km, kinh phí đi đường bộ là 3 USD/km. Hỏi người đó phải đi đường bộ một đoạn AD bao nhiêu để kinh phí đi từ A đến C nhỏ nhất? (AB vuông góc BC-hình dưới đây)
Cho tứ diện ABCD, có \(AB = AC = AD = a,\,\,\,BAD = {90^0};\,\,DAC = {60^0};\,\,CAB = {120^0}\). Thể tích tứ diện ABCD là
Khối lập phương ABCD.A’B’C’D’ có độ dài đoạn \(AB' = 2a\). Thể tích của khối đó là