Tìm tập xác định D của hàm số \(y = {\log _2}\left( { - {x^2} + 3x} \right)\)
D. \(D = \left( {0;3} \right)\)
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Phương pháp:
\(y = {\log _a}f\left( x \right)\) xác định \( \Leftrightarrow f\left( x \right) > 0\)
Cách giải:
ĐKXĐ: \( - {x^2} + 3x > 0 \Leftrightarrow 0 < x < 3\)
TXĐ: \(D
Đáp án C
Phương pháp:
Hàm số bậc nhất trên bậc nhất không có cực trị.
Cách giải:
Chọn phương án C. Do:
\(y = \frac{{x - 1}}{{x + 3}},\,\left( {D = R\backslash \left\{ 3 \right\}} \right) \Rightarrow y' = \frac{4}{{{{\left( {x + 3} \right)}^2}}} > 0,\,\,\forall x \in D\)
\(y = {x^4},\,\,\left( {D = R} \right) \Rightarrow y' = 4{x^3}\), hàm số đạt cực tiểu tại \(x = 0\)
\(y = {x^2} + 2x + 2,\,\,\left( {D = R} \right) \Rightarrow y' = 2x + 2\), hàm số đạt cực tiểu tại \(x = - 1\)
\(y = - {x^3} + x,\,\,\left( {D = R} \right) \Rightarrow y' = - 3{x^2} + 1\), hàm số đạt cực tiểu tại \(x = - \frac{1}{{\sqrt 3 }}\), hàm số đạt cực đại tại \(x = \frac{1}{{\sqrt 3 }}\)
= \left( {0;3} \right)\)
Tập nghiệm của bất phương trình \({2^{x + 2}} < {\left( {\frac{1}{4}} \right)^{ - x}}\) là
Giá trị thực của tham số m để đồ thị hàm số \(y = {x^4} - 2m{x^2} + m\) có ba điểm cực trị tạo thành một tam giác nhận gốc tọa độ làm trọng tâm là
Cho hàm số \(y = {x^3} - 3{x^2} + 2\). Gọi A, B là 2 điểm thuộc đồ thị hàm số đã cho có hoành độ lần lượt là \({x_A},\,{x_B}\), tiếp tuyến của đồ thị hàm số tại A, B song song với nhau và đường thẳng AB tạo với 2 trục tọa độ một tam giác cân, đường thẳng AB có hệ số góc dương. Tính \({x_A}{x_B}\).
Tìm tập hợp tất cả các giá trị của tham só thực m để hàm số \(y = \frac{{mx - 1}}{{x - m}}\) đồng biến trên từng khoảng xác định:
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số \(y = \frac{x}{{x - m\sqrt {4 - {x^2}} }}\) có ba tiệm cận đứng.
Cho hình trụ có diện tích toàn phần lớn hơn diện tích xung quanh là \(4\pi \). Bán kính đáy của hình trụ là
Trong không gian Oxyz, cho hai điểm \(A\left( {1;2;0} \right),\,\,\,B\left( {2; - 1;1} \right)\). Tìm điểm C có hoành độ dương trên trục Ox sao cho tam giác ABC vuông tại C.
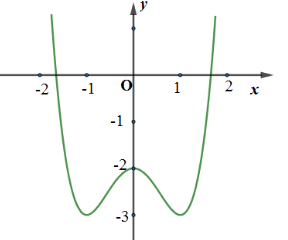
Đường cong trong hình vẽ bên là đồ thị của hàm số nào trong các hàm số dưới đây?
Cho bất phương trình \({2^{{x^2} + x}} + 2x \le {2^{3 - x}} - {x^2} + 3\) có tập nghiệm là \(\left[ {a;b} \right]\). Giá trị của \(T = 2a + b\) là:
Diện tích toàn phần của một hình hộp chữ nhật là \({S_{tp}} = 8{a^2}\). Đáy của hình hộp là hình vuông cạnh a. Tính thể tích V của khối hộp theo a.
Cho hình chóp S.ABCD có cạnh bên SA tạo với đáy một góc \({60^0}\) và \(SA = a\sqrt 3 \), đáy là tứ giác có hai đường chéo vuông góc, \(AC = BD = 2a\). Tính thể tích V của khối chóp theo a.
Hàm số nào trong bốn hàm số được liệt kê dưới đây không có cực trị?
Tìm tất cả các giá trị thực của tham số m để phương trình \({x^3} - {3^2} - m = 0\) có hai nghiệm phân biệt.
Cho hình nón tròn xoay có đường cao \(h = 4\) và diện tích đáy là \(9\pi \). Tính diện tích xung quanh của hình nón.