Cho đường tròn (O; R), đường kính AB và tiếp tuyến Ax. Từ điểm C thuộc Ax, kẻ tiếp tuyến thứ hai CD với đường tròn (O) (D là tiếp điểm). Gọi giao điểm của CO và AD là I.
a) Chứng minh: CO ⊥ AD.
b) Gọi giao điểm của CB và đường tròn (O) là E (E ≠ B). Chứng minh CE.CB = CI.CO.
c) Chứng minh: Trực tâm H của tam giác CAD di động trên đường cố định khi điểm C di chuyển trên Ax.
Giải bởi Vietjack
Lời giải
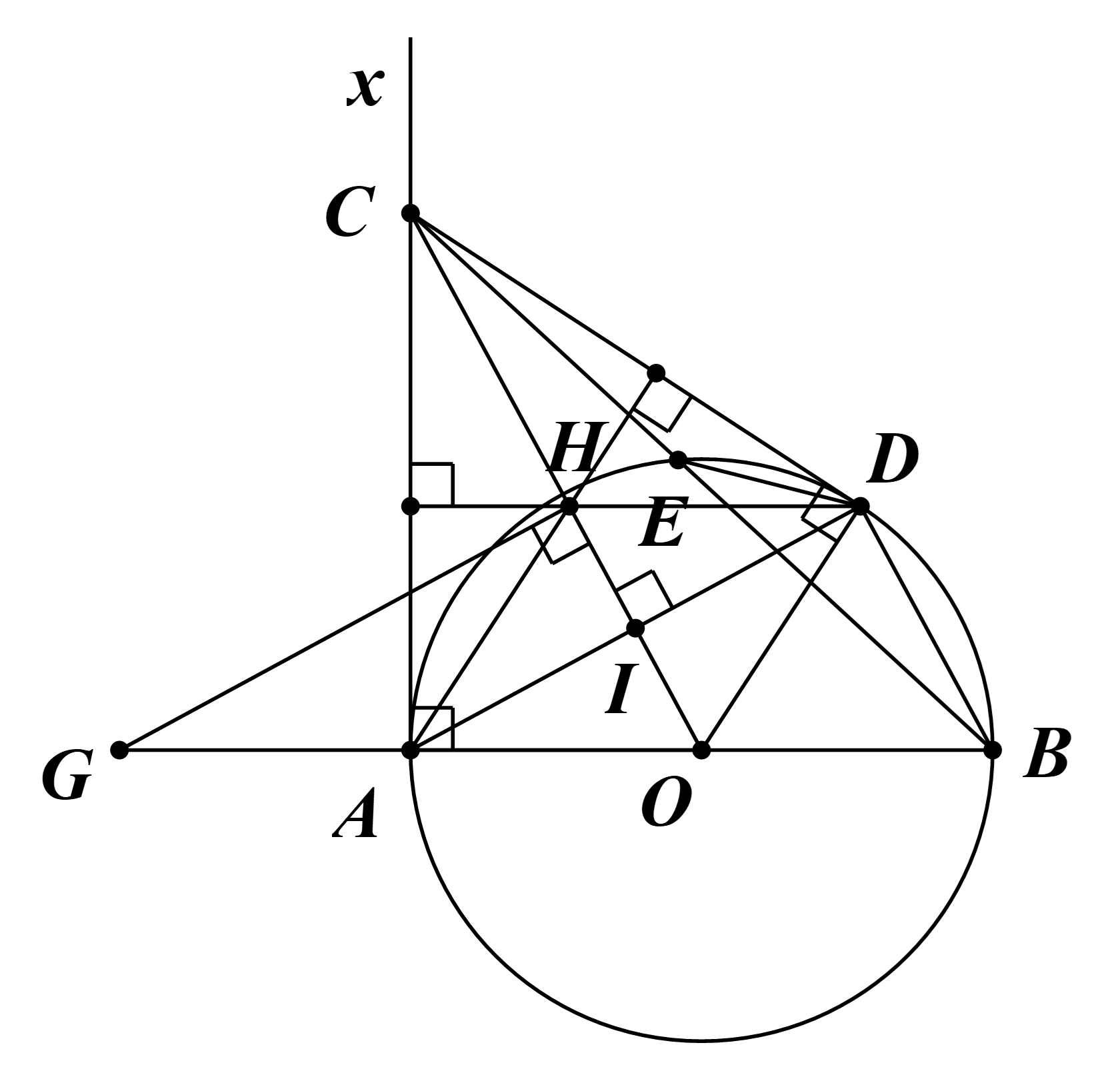
a) Ta có CA, CD là hai tiếp tuyến của (O) cắt nhau tại C.
Suy ra CA = CD.
Khi đó C nằm trên đường trung trực của đoạn thẳng AD (1)
Lại có OA = OD = R.
Suy ra O nằm trên đường trung trực của đoạn thẳng AD (2)
Từ (1), (2), suy ra CO là đường trung trực của đoạn thẳng AD.
Do đó CO ⊥ AD tại I.
b) Xét ∆CED và ∆CDB, có:
\(\widehat C\) chung.
\(\widehat {CDE} = \widehat {CBD}\) (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung).
Do đó (g.g).
Suy ra \(\frac{{CE}}{{CD}} = \frac{{CD}}{{CB}}\).
Do đó CE.CB = CD2 (3)
Xét ∆CDO vuông tại D có DI là đường cao:
CD2 = CI.CO (hệ thức lượng trong tam giác vuông) (4)
Từ (3), (4), suy ra CE.CB = CI.CO (điều phải chứng minh).
c) Ta có AH // OD (cùng vuông góc với CD) và DH // OA (cùng vuông góc với AC).
Suy ra tứ giác AHDO là hình bình hành.
Mà I là giao điểm của AD và HO.
Do đó I là trung điểm của HO.
Trên tia đối của tia AO, lấy điểm G sao cho A là trung điểm của GO.
Khi đó AI là đường trung bình của tam giác GHO.
Suy ra AI // GH.
Mà AI ⊥ HO (chứng minh trên).
Do đó GH ⊥ HO.
Suy ra \(\widehat {GHO} = 90^\circ \).
Vậy khi C di chuyển trên Ax thì trực tâm H của tam giác ACD di động trên đường tròn tâm A, bán kính AO cố định.
Cho tam giác ABC vuông tại A (AB < AC) có đường cao AH. Kẻ HD vuông góc với AB (D thuộc AB), kẻ HE vuông góc với AC (E thuộc AC).
a) Chứng minh tứ giác ADHE là hình chữ nhật.
b) Gọi I là trung điểm của đoạn thẳng HC. Gọi K là điểm đối xứng với điểm A qua điểm I. Chứng minh rằng AC // HK.
c) Chứng minh tứ giác DECK là hình thang cân.
d) Gọi O là giao điểm của DE và AH. Gọi M là giao điểm của AI và CO. Chứng minh \(AM = \frac{1}{3}AK\).
Cho tam giác ABC, I là giao điểm của 3 đường phân giác, đường thẳng vuông góc với CI tại I cắt AC và BC tại M và N.
a) Chứng minh AM.BI = AI.IM.
b) Chứng minh BN.AI = BI.NI.
c) Chứng minh \(\frac{{AM}}{{BN}} = {\left( {\frac{{AI}}{{BI}}} \right)^2}\).
Cho tam giác ABC. Gọi H là điểm đối xứng với B qua G với G là trọng tâm tam giác. Chứng minh:
a) \(\overrightarrow {AH} = \frac{2}{3}\overrightarrow {AC} - \frac{1}{3}\overrightarrow {AB} ;\,\overrightarrow {CH} = - \frac{1}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} \).
b) \(\overrightarrow {MH} = \frac{1}{6}\overrightarrow {AC} - \frac{5}{6}\overrightarrow {AB} \), với M là trung điểm BC.
Cho tam giác ABC, trên các đường thẳng BC, AC, AB lần lượt lấy các điểm M, N, P sao cho \(\overrightarrow {MB} = 3\overrightarrow {MC} ;\,\overrightarrow {NA} = 3\overrightarrow {CN} ;\,\overrightarrow {PA} + \overrightarrow {PB} = \vec 0\).
a) \(\overrightarrow {PM} ,\,\overrightarrow {PN} \) theo \(\overrightarrow {AB} ,\,\overrightarrow {AC} \).
b) Chứng minh M, N, P thẳng hàng.
Cho hai điểm A(3; –5), B(1; 0).
a) Tìm tọa độ điểm C sao cho \[\overrightarrow {OC} = - 3\overrightarrow {AB} \].
b) Tìm điểm D đối xứng của A qua C.
c) Tìm điểm M chia đoạn AB theo tỉ số k = –3.
Cho tam giác ABC, I là giao điểm của 3 đường phân giác. Đường thẳng qua I vuông góc với CI cắt AC và BC theo thứ tự tại M và N. Chứng minh rằng:
a) 
.
b) \(\frac{{AM}}{{BN}} = {\left( {\frac{{AI}}{{BI}}} \right)^2}\).
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB và O là 1 điểm tùy ý.
a) Chứng minh rằng: \(\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} = \vec 0\).
b) Chứng minh rằng \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} \).
Cho (O) và điểm I bên ngoài (O). Từ I vẽ một cát tuyến IAB với (O). Tiếp tuyến tại A và B cắt nhau tại M. AB cắt OM tại H.
a) Chứng minh: MA2 = MH.MO.
b) Từ M kẻ ME vuông góc OI tại E cắt (O) tại D và AB tại K. Chứng minh: IE.IO = IH.IK.
c) Chứng minh: ID là tiếp tuyến (O).
Cho hình bình hành ABCD, qua C kẻ đường thẳng song song BD cắt AB ở E, cắt AD ở F.
a) Tứ giác BECD là hình gì? Vì sao?
b) Chứng minh 3 đường thẳng AC, BF, DE đồng quy (cùng đi qua 1 điểm).
Cho A(2; 3), B(–1; –1), C(6; 0).
a) Tìm tọa độ các \(\overrightarrow {AB} ,\,\overrightarrow {AC} \). Từ đó chứng minh ba điểm A, B, C không thẳng hàng.
b) Tìm tọa độ trọng tâm G của tam giác ABC.
c) Tìm tọa độ điểm D để tứ giác ABCD là hình bình hành.
d) Tìm tọa độ điểm E thỏa mãn \(\overrightarrow {OE} + 3\overrightarrow {EB} - 3\overrightarrow {EA} = \vec 0\).
Cho đường tròn (O), đường kính AB. Trên tia tiếp tuyến Ax của đường tròn lấy điểm M (M ≠ A), từ M vẽ tiếp tuyến thứ hai MC với đường tròn (O) (C là tiếp điểm). Kẻ CH vuông góc với AB (H ∈ AB). MB cắt đường tròn (O) tại điểm Q (Q ≠ B) và cắt CH tại N. Gọi I là giao điểm của MO và AC.
a) Chứng minh AIQM là tứ giác nội tiếp.
b) Chứng minh OM // BC.
c) Chứng minh tỉ số \(\frac{{CH}}{{CN}}\) không đổi khi M di động trên tia Ax (M ≠ A).
Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a, có \(\widehat {BAD} = 60^\circ \) và \(SA = SB = SD = \frac{{a\sqrt 3 }}{2}\).
a) Tính khoảng cách từ S đến mặt phẳng (ABCD) và độ dài cạnh SC.
b) Chứng minh mặt phẳng (SAC) vuông góc với mặt phẳng (ABCD).
c) Chứng minh SB vuông góc với BC.
d) Gọi φ là góc giữa hai mặt phẳng (SBD) và (ABCD). Tính tanφ.
Từ điểm I nằm ngoài đường tròn (O), vẽ cát tuyến cắt đường tròn tại A và B (IA < IB). Các tiếp tuyến tại A và B cắt nhau tại M. OM cắt AB tại K.
a) Chứng minh K là trung điểm của AB.
b) Vẽ MH ⊥ OI tại H. Chứng minh OB2 = OH.OI.
c) Gọi N là giao điểm của AB và MH. Chứng minh IA.IB = IK.IN.
