Cho hàm số y = (2m – 1)x + 2 (1) có đồ thị là đường thẳng dm.
a) Vẽ đồ thị hàm số m = 1.
b) Tìm m để hàm số (1) đồng biến trên ℝ.
c) Tìm m để dm đồng quy với d1: y = x + 4 và d2: y = –2x + 7.
Giải bởi Vietjack
Lời giải
a) dm: y = (2m – 1)x + 2 \(\left( {m \ne \frac{1}{2}} \right)\).
Với m = 1, ta có: y = x + 2.
Bảng giá trị của dm khi m = 1:
Do đó đồ thị hàm số y = x + 2 là đường thẳng đi qua hai điểm (1; –1) và (0; 2).
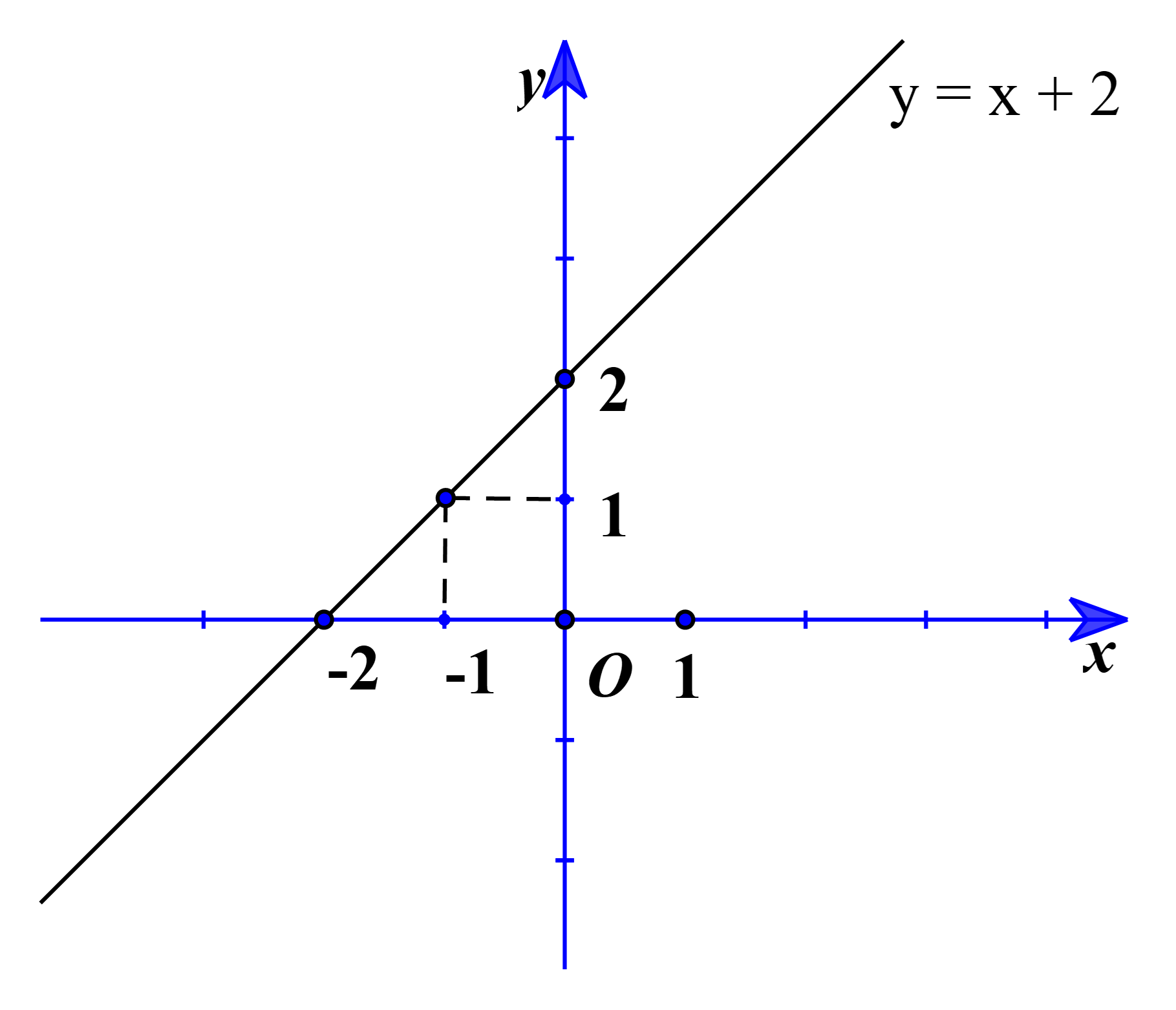
b) Hàm số (1) đồng biến trên ℝ ⇔ 2m – 1 > 0.
\( \Leftrightarrow m > \frac{1}{2}\).
Vậy \(m > \frac{1}{2}\) thỏa mãn yêu cầu bài toán.
c) Phương trình hoành độ giao điểm của d1 và d2: x + 4 = –2x + 7
⇔ 3x = 3 ⇔ x = 1.
Với x = 1, ta có y = 1 + 4 = 5.
Do đó giao điểm của d1 và d2 là A(1; 5).
Để ba đường thẳng d, d1 và d2 đồng quy thì A(1; 5) ∈ dm.
Û 5 = (2m – 1).1 + 2
Û 5 = 2m – 1 + 2
Û 2m = 4
Û m = 2 (nhận)
Vậy m = 2 thỏa mãn yêu cầu bài toán.
Qua điểm M nằm ngoài (O), vẽ tiếp tuyến MA (A là tiếp điểm) và cát tuyến MBC (tia MO nằm giữa hai tia MA và MB).
a) Chứng minh MA2 = MB.MC.
b) Kẻ AH vuông góc với OM tại H. Chứng minh MH.MO = MB.MC và tứ giác OHBC nội tiếp.
c) Tia BH cắt (O) tại điểm thứ hai là K. Chứng minh C đối xứng K qua đường thẳng OM.
Cho đường tròn (O; R), đường kính AB. Kẻ tiếp tuyến Ax và lấy trên tiếp tuyến đó một điểm P sao cho AP > R, từ P kẻ tiếp tuyến tiếp xúc với (O) tại M.
1) Chứng minh rằng A, P, M, O cùng thuộc một đường tròn.
2) Chứng minh BM song song với OP.
3) Đường thẳng vuông góc với AB ở O cắt tia BM tại N. Chứng minh tứ giác OBNP là hình bình hành.
4) Biết AN cắt OP tại K, PM cắt ON tại I; PN và OM kéo dài cắt nhau tại J. Chứng minh I, J, K thẳng hàng.
Cho hình thoi ABCD có AB = BD. Gọi M, N lần lượt trên các cạnh AB, BC sao cho AM + NC = AD.
1) Chứng minh AM = BN.
2) Chứng minh ∆AMD = ∆BND.
3) Tính số đo các góc của ∆DMN.
Cho hình vuông ABCD có cạnh bằng a. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. M là giao điểm của CE và DF.
a) Chứng minh tứ giác EFGH là hình vuông.
b) Chứng minh DF ⊥ CE và ∆MAD cân.
c) Tính diện tích tam giác MDC theo a.
Cho hình vuông ABCD cạnh a, M bất kì. Chứng minh rằng các vectơ sau là vectơ không đổi. Tính độ dài của chúng:
a) \(2\overrightarrow {MA} - \overrightarrow {MB} - \overrightarrow {MC} \).
b) \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} - 3\overrightarrow {MD} \).
c) \(4\overrightarrow {MA} - 3\overrightarrow {MB} + \overrightarrow {MC} - 2\overrightarrow {MD} \).
Viết phương trình của đường thẳng y = ax + b thỏa mãn một trong các điều kiện sau:
a) Có hệ số góc bằng –2 và đi qua điểm A(–1; 2).
b) Có tung độ gốc bằng 3 và đi qua một điểm trên trục hoành có hoành độ bằng –1.
c) Đi qua hai điểm B(1; 2) và C(3; 6).
Cho hàm số bậc nhất: y = (2m + 1)x – 2 có đồ thị là đường thẳng (d).
a) Vẽ đồ thị hàm số với m = 1.
b) Tìm m để (d) song song với đồ thị hàm số: y = –4x + 1.
c) Tìm m để khoảng cách từ gốc tọa độ đến (d) bằng \(\sqrt 2 \).
Cho đường tròn (O; R) có hai dây AB, CD vuông góc với nhau ở M. Biết AB = 14 cm; CD = 12 cm; MC = 2 cm. Bán kính R và khoảng cách từ tâm O đến dây CD lần lượt là
Công ty Bao bì Dược cần sản xuất 3 loại hộp giấy: đựng thuốc B1, đựng cao Sao vàng, và đựng “Quy nhân sâm đại bổ hoàn”. Để sản xuất các loại hộp này, công ty dùng các tấm bìa có kích thước giống nhau. Mỗi tấm bìa có hai cách cắt khác nhau:
– Cách thứ nhất cắt được 3 hộp B1, 1 hộp cao Sao vàng và 6 hộp Quy sâm.
– Cách thứ hai cắt được 2 hộp B1, 3 hộp cao Sao vàng và 1 hộp Quy sâm.
Theo kế hoạch, số hộp Quy sâm phải có là 900 hộp, số hộp B1 tối thiểu là 900 hộp, số hộp cao Sao vàng tối thiểu là 1000 hộp. Cần phương án sao cho tổng số bìa phải dùng là ít nhất?
Cho nửa đường tròn (O) đường kính CD. Vẽ các tiếp tuyến Cx, Dy (Cx, Dy và nửa đường tròn (O) thuộc cùng một nửa mặt phẳng bờ CD). Lấy điểm M tùy ý trên nửa đường tròn trên. Tiếp tuyến tại M cắt Cx, Dy lần lượt tại A, B.
a) Chứng minh ∆OAB vuông tại O.
b) Chứng minh AB = AC + BD.
c) Chứng minh CD là tiếp tuyến của đường tròn đường kính AB.
Cho biểu thức \(P = \frac{{2{x^2}}}{{{x^2} - 1}} + \frac{x}{{x + 1}} - \frac{x}{{x - 1}}\).
a) Tìm x để biểu thức P có nghĩa.
b) Rút gọn P.
c) Tính P tại x = –3.
d) Tìm giá trị nguyên của x để P có giá trị nguyên.
Cho hình thang cân ABCD (AB // CD) có đường chéo BD chia hình thang thành hai tam giác cân: tam giác ABD cân tại A và tam giác BCD cân tại D. Tính các góc của hình thang cân đó.
