Một quả cầu nặng m = 100 g được treo ở đầu một sợi dây nhẹ, không co dãn, dài l = 1 m (đầu kia của dây cố định). Truyền cho quả cầu ở vị trí cân bằng một vận tốc đầu v0 theo phương ngang. Khi dây treo nghiêng góc α =300 so với phương thẳng đứng thì gia tốc của quả cầu có phương ngang. Cho g = 10 m/s2, bỏ qua mọi ma sát.
a) Tìm vận tốc v0.
b) Tính lực căng dây và vận tốc của vật tại vị trí có góc lệch a = 400.
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
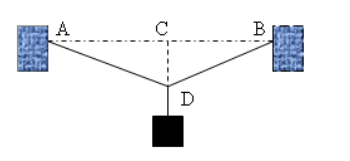
a. Khi dây treo nghiêng góc \(\alpha = {30^0}\) so với phương thẳng đứng, vật M chịu tác dụng của các lực như hình vẽ. Do gia tốc có phương ngang nên
T . cos 300 = m.g (1)
Mặt khác, xét theo phương hướng tâm MO ta có:
\(T - mg.cos{30^0} = \frac{{m{v^2}}}{\ell }\) (2) (Với v là vận tốc của vật tại M)
Từ (1) và (2) suy ra: \({v^2} = \frac{{g\ell }}{{2\sqrt 3 }}\,\,(3)\)
Áp dụng ĐLBT cơ năng cho hệ khi vật ở vị trí M và khi vật ở vị trí cân bằng ta được:
\(v_0^2 = {v^2} + 2g\ell \left( {1 - cos{{30}^0}} \right) = \frac{{12 - 5\sqrt 3 }}{6}g\ell \)
\( \Rightarrow {v_0} = 2,36\,m/s\)
b. Áp dụng ĐLBT cơ năng cho hệ khi vật ở vị trí \(\alpha = {40^0}\)và khi vật ở vị trí cân bằng ta được:
\(v_0^2 = {v^2} + 2g\ell \left( {1 - cos{{40}^0}} \right)\)\( \Rightarrow v = \sqrt {v_0^2 - 2g\ell \left( {1 - cos{{40}^0}} \right)} \approx 0,94\,m/s\)
Xét theo phương sợi dây ta có:
T = m.g.cos400 + \(\frac{{m{v^2}}}{\ell }\)= 0,1.10.cos400 + \(\frac{{{{0,1.0,94}^2}}}{1} = 0,86\,N\)
Một vật được ném từ một điểm M ở độ cao h = 45 m với vận tốc ban đầu vo = 20 m/s lên trên theo phương hợp với phương nằm ngang một góc 450. Lấy g = 10 m/s2, bỏ qua lực cản của không khí. Hãy xác định:
a. Quỹ đạo của vật, độ cao cực đại vật đạt đươc so với mặt đất và thời gian vật bay trong không khí.
b. Tầm bay xa của vật, vận tốc của vật khi chạm đất.
c. Xác định thời gian để vật có độ cao 50 m và xác định vận tốc của vật khi đó.
Hai xe I và II chuyển động trên cùng một đường thẳng tại hai điểm A và B. Biết tốc độ xe I và xe II lần lượt là 50 km/h và 30 km/h. Tính vận tốc tương đối của xe I so với xe II khi:
a) Hai xe chuyển động cùng chiều.
b) Hai xe chuyển động ngược chiều.
Hai gương phẳng G1, G2 quay mặt phản xạ vào nhau và tạo với nhau một góc 600. Một điểm S nằm trong khoảng 2 gương.
a. Hãy nêu cách vẽ đường đi của tia sáng phát ra từ S phản xạ lần lượt qua G1, G2 rồi quay trở lại S.
b. Tính góc tạo bởi tia xuất phát từ S và tia phản xạ đi qua S.
Một người kéo một thùng nước có khối lượng 12 kg từ giếng sâu 8 m. Lấy g = 10 m/s2.
a) Tính công và công suất của người khi kéo đều thùng nước hết 16 s.
b) Nếu dùng máy để kéo thùng nước nói trên đi lên nhanh dần đều và thời gian kéo mất 2 s thì công và công suất của máy bằng bao nhiêu?
Một vật khối lượng m = 1 kg được kéo chuyển động ngang bởi một lực \(\vec F\) hợp với phương ngang một góc \(\alpha \)= 30° và có độ lớn F = 2 N. Biết khi bắt đầu chuyển động được 2 s vật đi được quãng đường 1,66 m. Cho g = 10 m/s2, \(\sqrt 3 = 1,73\).
a, Tính hệ số ma sát trượt giữa vật và mặt sàn.
b, Tính hệ số ma sát với lực kéo nói trên vật chuyển động thẳng đều.
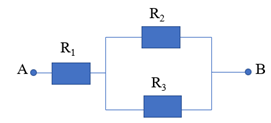
Có mạch điện như hình vẽ: \({R_1} = 8\Omega ;\,{R_2} = 6\Omega ;\,{R_3} = 12\Omega \). Hiệu điện thế UAB = 24 V.
a. Tính cường độ dòng điện qua mỗi điện trở.
b. Tính công suất tỏa nhiệt của đoạn mạch.
c. Tính nhiệt lượng tỏa ra của điện trở R3 trong thời gian 10 phút.